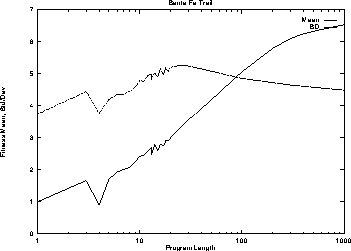
Figure 7: Mean and Standard Deviation of program scores vs. length
Why Ants are
Previous: Fitness Landscape
In this section we consider the fitness of fixed length schema [Poli and Langdon1997] within the program space. Unlike conventional schema analysis we define a schema's fitness as the mean score for all programs matching the schema. From this analysis it is evident that typically there is a large variation of program scores within a schema, typically the standard deviation of score is about the same as or larger than the schema's fitness. Thus a finite sample (such as a GA population) can only reliably be used to estimate the fitness of a schema if it contains multiple independent samples from the schema. If the GA is to reliably choose between schema based on its estimate of their fitness, the number of samples (i.e. programs) must be even bigger where the schema have similar fitness. (Of course the assumption that programs are independent is not justified after selection etc.)
The competetion between schema can be viewed as a heirarchy of competetions. The outermost level being between different lengths, then between different shapes of the same length (hyperspaces) and finally between different schema of the same shape. Figure 7 shows the Ant problem is difficult at the outermost level. The region containing the highest concentration of solutions (length=18) has a fitness of 2.9 but longer programs are on average fitter than this. While the standard deviation is large compared to the mean, a typical initial GP population is likely to be large enough to be able to reliably prefer solutions longer than 18 over those of length 18.

Figure 7:
Mean and Standard Deviation of program scores vs. length
Figure 8 shows the distribution of schema fitness for one of the hyperspaces containing solutions of length 11. (The other two hyperspaces are similar). Looking at the order zero schema, i.e. the hyperspace, we see it has a fitness above the average for programs of the same length, however there are other hyperspaces which are fitter.
Comparing schema of the same order we see, apart from order 9 (i.e. programs) there are always schema outside the hyperspace with higher fitness. However within the hyperspace, for a given order, the fittest schema is always one containing a solution. (Prog3 is the only function which takes three arguments. If a program's shape is given and it contains three way branches, then there must be a Prog3 at these points. I.e. the location of Prog3 are fixed. Therefore we exclude Prog3 from the schema order). It was feasible to consider all schema of order 2 or less. As Figure 8 shows there are many schema which do not contain a solution which are fitter than many of the same order that do. Also there are small components of solutions with below average fitness. It is not until more than five components have been assembled that all schema containing solutions have above average fitness. I.e. using a fixed representation solutions of length 11 cannot be assembled from small building blocks (low order schema) of above average fitness.

Figure 8:
Distribution of Schema fitness within a Hyperspace of length 11
containing a solution
Turning to programs of length 12, cf. Figure 9, looking at order zero we see a similar picture to length 11: hyperspaces containing solutions have fitness above the average for programs of the same length, however there are other hyperspaces which are fitter.
Comparing schema of the same order we see, apart from order 11 (i.e. programs) there are always schema outside the hyperspace with higher fitness. Also (unlike length 11) within the hyperspace the fittest schema of each order for orders 4--8 does not contain a solution. As with length 11, there are many schema which do not contain a solution which are fitter than many of the same order that do. Also there are small components of solutions with below average fitness. It is not until more than six components have been assembled that all schema containing solutions have above average fitness.

Figure 9:
Distribution of Schema fitness within a Hyperspace of length 12
containing a solution
Turning to programs of length 13 the situation is complicated by the much larger number of solutions and their diverse nature. We have selected three hyperspaces which contain solutions of different types, cf. Figures 10, 11 and 12. (Only data for schema of order, 0, 1 and 2 is available).
Looking at order zero we see a similar picture to length 12: the three selected hyperspaces have fitness above the average for programs of the same length, however (apart from the hyperspace chosen because it has the highest fitness) there are other hyperspaces which are fitter.
Comparing schema of the same order we see there are always schema outside the hyperspace with higher fitness (although the difference is small for the fittest hyperspace). As with lengths of 11 and 12, in two hyperspaces the fittest schema of order 0, 1, and 2 contain a solution (cf. Figures 10 and 12). However in the fittest hyperspace (Figure 11) the fittest schema of order 1 and 2 do not contain solutions. As with lengths 11 and 12, there are many schema which do not contain a solution which are fitter than many of the same order that do. Also there are small components of solutions with below average fitness.

Figure 10:
Distribution of Schema fitness within a Hyperspace of length 13
containing a (two move) solution

Figure 11:
Distribution of Schema fitness within a highest fitness Hyperspace of length 13
containing a solution

Figure 12:
Distribution of Schema fitness within a Hyperspace of length 13
containing a (intron) solution
Why Ants are
Previous: Fitness Landscape