


Next: Discussion
Up:
Why Ants are
Previous: Fixed Length Schema
We have analysed the shorter solutions
(cf. Figures 13 to 16).
As we shall see
all the solutions of length 11 and 12 and most of those of length
13 are variations of each other.
Figure 13 shows all the solutions of length 11.
There are twelve solutions of length 11.
Not only are they genetically distinct but they cause different
behaviour by the ant.
However we can recogise certain symmetries.
For example they contain pairs of ant rotate operations and it is no
surprise that these can be either pairs of Left or pairs of
Right terminals.
Another symmetry is that the program consists of three parts
which have to be performed in order but
the ant can start with any one of the three and still traverse the
trail.
Since the solution codes each of these as an argument of the root,
the root's arguments can be rotated.
Each rotation gives rise to a genetically different program, with
slightly different behaviour.
Each gives rise to a different tree shape and so the 12 solutions lie
in three distinct hyperspaces.
The solutions of length 12 are the same as those of length 11.
They are made one node longer by replacing a single Prog3 function
with two Prog2
(cf. Figure 14).
There are a total of four ways of doing this for each solution of
length 11
giving rise to 48 solutions of length.
While these are genetically distinct from each other and the solutions
of length 11
they represent identical behaviour.
There are 12 tree shapes (hyperspaces) each containing 4 solutions.
Extending this we can see that there must also be 48 solutions of
length 13 created by replacing both Prog3 with Prog2
(there are four ways of arranging the Prog2).
However there are other ways to make use of the available space to
represent the same solutions.
This is done by adding introns.
Each of the non-Prog3 nodes can be replaced by an IfFoodAhead one of
whose arguments is the previous node (and its arguments) and the other
is either a terminal which is identical to the other argument or is
never executed
(cf. Figure 15).
Most solutions of length 13 are of this type.
Thirteen nodes allow solutions of a different type which consecutively
performs two moves before looking for food
(cf. Figure 16).
Again there is symmetry in that the ant can be rotated either to the
right or to the left
but whichever is done first the opposite must be done in the later
part of the program.
This give rise to programs of the same shape with the same score.
The program now consists of five parts which have to be executed in
the correct order but,
as with solutions of length 11,
it does not matter which is first.
Each of these five orderings gives rise to a different behaviour but
each traverse the trail.
(However they take slightly different amounts of energy to do so.
Including energy as part of the fitness measure would give a means of
breaking the symmetry of these solutions).
Additionally there are three ways to arrange the arguments of the two
Prog3 which are functionally identical.
Each of these rearrangements yields solutions of different shapes.
Most of the other solutions of length 13 also perform two consecutive
Move operations.
These and the remaining solution of length 13
have less symmetry and
are fewer in number.
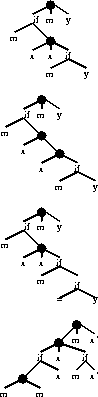
Figure 16:
Solutions of length 13 performing two Moves.
x can be either Left or Right but then 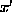 must rotate in the
opposite direction,
again the arguments of the root can be rotated and
there are equivelent ways to order the arguments of the two Prog3.
must rotate in the
opposite direction,
again the arguments of the root can be rotated and
there are equivelent ways to order the arguments of the two Prog3.
Figure 15:
Intron solution of length 13.
Like solutions of length 11
(x and y can be either Left or Right,
the three arguments of the root can be rotated)
and the = can be any terminal as it is never executed.
Figure 14:
Solutions of length 12.
Like solutions of length 11
(x and y can be either Left or Right,
the three arguments of the root can be rotated)
additionally one Prog3 is replaced by two Prog2
giving 48 solutions.
Figure 13:
Solutions of length 11.
x and y can be either Left or Right
and the three arguments of the root can be rotated,
giving 12 solutions.



Next: Discussion
Up:
Why Ants are
Previous: Fixed Length Schema
William B Langdon
Tue Feb 3 19:53:29 GMT 1998

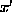 must rotate in the
opposite direction,
again the arguments of the root can be rotated and
there are equivelent ways to order the arguments of the two Prog3.
must rotate in the
opposite direction,
again the arguments of the root can be rotated and
there are equivelent ways to order the arguments of the two Prog3.