 neighbours).
neighbours).
Why Ants are
Previous: Comparison with Other
We consider two programs in the program space to be neighbours if they have the same shape and one can be obtained from the other just by changing one node. I.e. they are neighbours if making a point mutation to one program produces the other. This is the simplest neighbour relationship which means we can avoid the complications inherent in crossover operator such as GP crossover.
In the case of small programs (i.e. size 11, 12 and 13) we investigated the neighbourhoods of all the fitter programs, i.e. those with scores above 24 (in [Langdon1998b] in almost all runs the best individual found had a score better than 24). As expected this showed many neighbours are worse or much worse (i.e. score less than 24). It also showed that many individuals with fitness between 24 and 88 are local optima, in that none of their neighbours are fitter than them. With short programs only a few neigbours have identical fitness.
The neighbourhoods of solutions are composed of low fitness programs. For programs of length 11 or 12, apart from programs which score 24--27 or 36, all neighbours of the solutions score <24. I.e. if a hill climber searching programs of length 11 or 12 finds a program scoring more than 36 we know it will never find a solution, without restarting. (Figure 6 shows 50 runs of a variable length representation hill climber [Langdon1998b] most of which became trapped at suboptimal peaks. Similar behaviour is also seen with other search techniques such as GP). There are many more solutions of length 13 and they are structurally and operationally more diverse. So their neighbourhoods are also much bigger and more diverse and include programs with scores of 24--46, 52, 54, 63, 85, 87 and 88. However five times as many have scores below 24.
For longer programs exhaustive enumeration of the landscape is not feasible and we used Monte Carlo sampling. As before programs of a chosen length where sampled uniformly at random. Due to the rarity of high scoring programs only a small number (up to 19) with scores 24--89 where chosen and all their neighbours where created and tested.
Figure 4 shows for most program sizes and
most fitness values there are a large
number of programs which do not have any fitter neighbours.
In contrast Figure 5 shows the average number of neighbours
with the same fitness grows with program size.
These same fitness neighbours displace those that are worse,
and for the longest sizes almost all programs of intermediate fitness
have a large number of neighbours with the same score.
(In the Ant problem a program of length l
has approximately  neighbours).
neighbours).
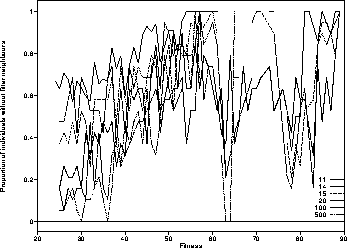
Figure 4:
Proportion of programs without fitter neighbours
for various program lengths.
(High noise Monte Carlo estimates ignored).
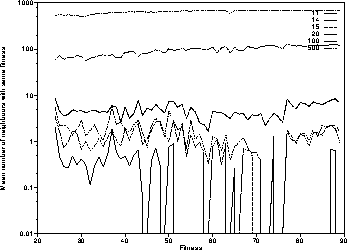
Figure 5:
Mean number of neighbours with same score for various program lengths.
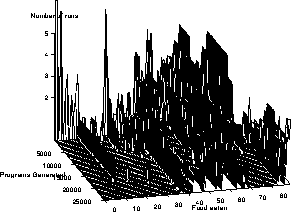
Figure 6:
Evolution of best fitness in 50
hill climbing runs using 50%--150% tree mutation
Why Ants are
Previous: Comparison with Other