


Next: Even-6 Parity and
Up: Boolean Program Spaces
Previous: 3 Input Boolean
It is not possible to analyse all the Boolean functions with more than
three inputs.
Instead we have concentrated on what are generally considered to be
the easiest and hardest Boolean functions of six inputs.
Namely the always-on-6 function and the even-6 parity function.
Figures 8 and 9 show the proportion of programs of
various lengths with each of the possible scores.
Figures 10 and 11 show the same when XOR is
added to the function set.
It is clear all four problems have the same near independence of
fitness from length.
Figure 9 shows a huge peak with 90% of points in the search
space having a fitness on the even-6 parity problem of exactly half marks, i.e. 32.
The number of programs with other scores falls exponentially away
either side of the peak.
Even sampling 10,000,000 points per length,
only three programs (1 with 27 and two with 37) were found outside the
range  hits.
[Rosca1997, Figure 4.1,] reports similar behaviour on the
even-5-parity problem.
(Note that he used ramped-half-and-half,
only sampled 16,000 programs
and did not consider variation of the fitness distribution with length).
He reports that the fitness distribution for the even-5-parity problem
are even more tightly grouped in a range of 5
values.
This could be due to the smaller study size
but allowing for this, the comparable range for even-6
parity still spans 7 values.
Looking at the short programs in Figure 9 shows they have an
even tighter distribution of fitness.
If this is also true for the even-5 parity problem then
the range reported in [Rosca1997] will be due to the larger of
the trees he sampled, particularly the full trees.
It seems reasonable to suggest that
the difference between a range of fitness values
reported by [Rosca1997] on the even-5 parity problem (5) and
that we find on the even-6 parity problem (7 or 9) is indeed due to the
peak in the fitness distribution being wider,
rather than an artifact of the bias inherent in ramped-half-and-half.
hits.
[Rosca1997, Figure 4.1,] reports similar behaviour on the
even-5-parity problem.
(Note that he used ramped-half-and-half,
only sampled 16,000 programs
and did not consider variation of the fitness distribution with length).
He reports that the fitness distribution for the even-5-parity problem
are even more tightly grouped in a range of 5
values.
This could be due to the smaller study size
but allowing for this, the comparable range for even-6
parity still spans 7 values.
Looking at the short programs in Figure 9 shows they have an
even tighter distribution of fitness.
If this is also true for the even-5 parity problem then
the range reported in [Rosca1997] will be due to the larger of
the trees he sampled, particularly the full trees.
It seems reasonable to suggest that
the difference between a range of fitness values
reported by [Rosca1997] on the even-5 parity problem (5) and
that we find on the even-6 parity problem (7 or 9) is indeed due to the
peak in the fitness distribution being wider,
rather than an artifact of the bias inherent in ramped-half-and-half.
The fitness distribution of the even-6 parity problem is
much tighter than that of the binomial distribution that would
be produced by selecting Boolean functions uniformly at random from
the 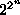 available.
I.e. centred on
available.
I.e. centred on  with variance of
with variance of 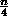 [Rosca1997, page 62,].
The measured variance
[Rosca1997, page 62,].
The measured variance
is only 0.12
rather than 1.5.
Such a tight fitness distribution
and in particular the absence of a high fitness tail
suggests that the problem will be hard for any adaptive algorithm.
As expected adding XOR to the function set greatly increases
the even-6 parity fitness distribution's width
and it retains its near independence of program size
(see Figure 11).
The standard deviation is now
0.92
rather than 0.34.
However the more dramatic effect of the wider distribution is the
number of solutions (i.e. programs scoring 64 hits)
is now measurable and is about 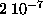 .
.
Figure 8 shows the distribution of number of trues returned
is a saw toothed curve.
The proportion of programs which have one of the odd scores on the
always-on-6 problem is about
0.3%.
The proportion which have an even score, not divisible by four, is about
1%,
scores divisible
by 4 about 2%,
those by 8 3%,
those by 16 6%
and
those by 32 10%.
Note the central peak in the even-6 parity fitness distribution
(see Figure 9)
is not solely due to a large number of programs which implement always-on-6 or
always-off-6.
Only 18.6%
of programs are of these two types.

:
Number of ones returned by 6-input Boolean functions
(note linear scale)

:
Even-6 parity program space
Figure 10 shows the distribution of number of trues returned
when XOR is added to the function set is a little changed
(cf. Figure 8)
but retains
its saw toothed appearance and near independence of program size.

:
Number of ones returned by 6-input Boolean functions,
XOR included
(note linear scale)

:
Even-6 parity program space,
including XOR in function set



Next: Even-6 Parity and
Up: Boolean Program Spaces
Previous: 3 Input Boolean
William B Langdon
Tue Jun 16 15:05:48 BST 1998
 hits.
[Rosca1997, Figure 4.1,] reports similar behaviour on the
even-5-parity problem.
(Note that he used ramped-half-and-half,
only sampled 16,000 programs
and did not consider variation of the fitness distribution with length).
He reports that the fitness distribution for the even-5-parity problem
are even more tightly grouped in a range of 5
values.
This could be due to the smaller study size
but allowing for this, the comparable range for even-6
parity still spans 7 values.
Looking at the short programs in Figure 9 shows they have an
even tighter distribution of fitness.
If this is also true for the even-5 parity problem then
the range reported in [Rosca1997] will be due to the larger of
the trees he sampled, particularly the full trees.
It seems reasonable to suggest that
the difference between a range of fitness values
reported by [Rosca1997] on the even-5 parity problem (5) and
that we find on the even-6 parity problem (7 or 9) is indeed due to the
peak in the fitness distribution being wider,
rather than an artifact of the bias inherent in ramped-half-and-half.
hits.
[Rosca1997, Figure 4.1,] reports similar behaviour on the
even-5-parity problem.
(Note that he used ramped-half-and-half,
only sampled 16,000 programs
and did not consider variation of the fitness distribution with length).
He reports that the fitness distribution for the even-5-parity problem
are even more tightly grouped in a range of 5
values.
This could be due to the smaller study size
but allowing for this, the comparable range for even-6
parity still spans 7 values.
Looking at the short programs in Figure 9 shows they have an
even tighter distribution of fitness.
If this is also true for the even-5 parity problem then
the range reported in [Rosca1997] will be due to the larger of
the trees he sampled, particularly the full trees.
It seems reasonable to suggest that
the difference between a range of fitness values
reported by [Rosca1997] on the even-5 parity problem (5) and
that we find on the even-6 parity problem (7 or 9) is indeed due to the
peak in the fitness distribution being wider,
rather than an artifact of the bias inherent in ramped-half-and-half.
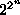 available.
I.e. centred on
available.
I.e. centred on  with variance of
with variance of 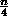 [
[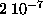 .
.



