 wbl).
wbl).
Recall that the fitness of a program is determined by the closeness of the function the program actually implements and the target function. E.g if the program implements function 0 (always return false) its fitness when searching for 3 input rule 150 (3-even parity) is 4, since it gets half of the 8 test cases right. That is for each target function there is a fixed simple mapping between the function implement by a program and the program's fitness. So the functionality of a trial solution readily gives its fitness on all the Boolean problems. Therefore by considering the distribution of the functionality of each point in the search space, we can consider simultaneously the fitness distribution of all of the Boolean functions.
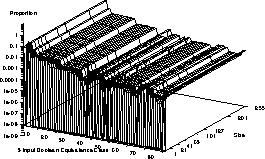
In this section we consider all the Boolean functions for n=3. There are 256 of them but they can be split into 80 equivalence classes. Functions are equivalent if permuting their inputs can produce the same functionality. By symmetry members of the same equivalence class will occur in the same numbers in the search space. Therefore we need only consider one representative function from each class [Koza1992, page 215,].
Figure 3 shows the number of examples of each
function found when
10 million trees of length 41 were created at random.
(The 80 equivalence classes are ordered along the x-axis in order of
decreasing frequency).
As expected there is good agreement with [Koza1992, Table 9.3,].
Figure 4 shows similar plots for a wide range of lengths.
(Data for lengths 1, 3, 5, 7, 9, 11 and 13 were gathered by evaluating
every tree of that length,
whereas data for larger trees was gathered by randomly sampling
10 million programs for each length.
C++ code to generate random programs is available via
http://www.cs.bham.ac.uk/ wbl).
wbl).

Figure 3:
Number of functions of length 41 in each equivalence class
Figure 4 shows a certain minimum size is required
before the problem can be solved and
that the minimum size depends on the difficulty of
the problem. Once this threshold size is exceeded the proportion of
programs which belong to the equivalence class grows rapidly to a
stable value which appears to be more-or-less independent of program
size.
Figure 5 shows these characteristics are retained if
we extend the function set to include XOR.
(Adding XOR to the function set greatly extends the search space and
so enumerating all trees of length 13 is no longer feasible, therefore
data for length 13 was produced by random sampling).
Note adding the XOR function radically changes the program
space.
In particular, as might be expected, the two parity functions
(equivalence classes 79 and 80) are much
more prevalent.
Also the range of frequencies is much reduced.
For example
68 of the 80 equivalence classes
have frequencies between 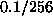 and
and  rather than 28 with the standard function set.
rather than 28 with the standard function set.

:
Proportion of functions in each equivalence class
:
Proportion of functions in each equivalence class
with XOR in function set
While Figures 4 and 5 can be used to estimate the fitness space of each three input Boolean function across the whole space, there are some interesting parts of these spaces where certain functions are more concentrated than elsewhere. Figure 6 plots the proportion of full trees of different depths which implement the parity functions. It is clear there are far more parity functions amongst the full trees than there are on average. When XOR is added to the function set, see Figure 7, there are again a higher proportion of parity functions but the difference between the full trees and the rest of the search space is less dramatic.
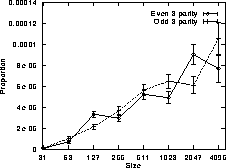
Figure 6:
3 input parity functions in full trees
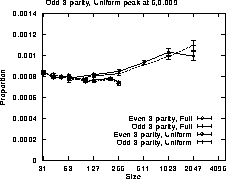
Figure 7:
Proportion of 3 input parity functions in full trees with XOR