


Next: Boolean Program Spaces
Up: Boolean Functions Fitness Spaces
Previous: Introduction
The Boolean functions have often been used as benchmark problems.
The program trees we will consider are composed of n terminals
(D0, D1, ... D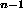 ) which are the Boolean inputs to the program
and the Boolean logic functions AND, OR, NAND and NOR
[Koza1992].
These are sufficient to construct any Boolean function
but we shall also investigate including the exclusive-or function (XOR).
Note [Koza1992] required all the functions to have the same
arity,
this is not required in our approach.
The fitness of each tree is given by evaluating it as a logical
expression for each of the
) which are the Boolean inputs to the program
and the Boolean logic functions AND, OR, NAND and NOR
[Koza1992].
These are sufficient to construct any Boolean function
but we shall also investigate including the exclusive-or function (XOR).
Note [Koza1992] required all the functions to have the same
arity,
this is not required in our approach.
The fitness of each tree is given by evaluating it as a logical
expression for each of the 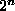 possible combinations of D
possible combinations of D inputs.
Its fitness is the number of fitness cases when its output
agrees with that of the target Boolean function.
inputs.
Its fitness is the number of fitness cases when its output
agrees with that of the target Boolean function.
There are
 different trees of length l
[Koza1992, page 213,] [Alonso and Schott1995].
|F| is four (or five if XOR is included).
(Note this formula is simple as each function (internal node) has
two arguments).
The number of programs rises rapidly (approximately
exponentially) with increasing program length l
(see Figures 1 and 2).
Of course if no bounds are placed on the size or depth of programs
then the number of them is unbounded,
i.e. the search space is infinite.
different trees of length l
[Koza1992, page 213,] [Alonso and Schott1995].
|F| is four (or five if XOR is included).
(Note this formula is simple as each function (internal node) has
two arguments).
The number of programs rises rapidly (approximately
exponentially) with increasing program length l
(see Figures 1 and 2).
Of course if no bounds are placed on the size or depth of programs
then the number of them is unbounded,
i.e. the search space is infinite.
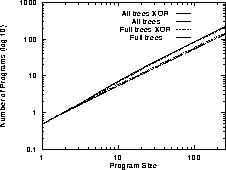
Figure 1:
Size of 3-Input Boolean Function Search Spaces (note log log scale)
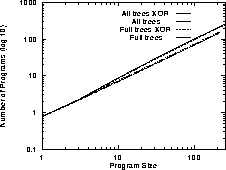
Figure 2:
Size of 6-Input Boolean Function Search Spaces (note log log scale)
William B Langdon
Tue Jun 16 15:05:48 BST 1998
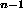 ) which are the Boolean inputs to the program
and the Boolean logic functions AND, OR, NAND and NOR
[Koza1992].
These are sufficient to construct any Boolean function
but we shall also investigate including the exclusive-or function (XOR).
Note [Koza1992] required all the functions to have the same
arity,
this is not required in our approach.
The fitness of each tree is given by evaluating it as a logical
expression for each of the
) which are the Boolean inputs to the program
and the Boolean logic functions AND, OR, NAND and NOR
[Koza1992].
These are sufficient to construct any Boolean function
but we shall also investigate including the exclusive-or function (XOR).
Note [Koza1992] required all the functions to have the same
arity,
this is not required in our approach.
The fitness of each tree is given by evaluating it as a logical
expression for each of the 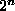 possible combinations of D
possible combinations of D inputs.
Its fitness is the number of fitness cases when its output
agrees with that of the target Boolean function.
inputs.
Its fitness is the number of fitness cases when its output
agrees with that of the target Boolean function.
 different trees of length l
[
different trees of length l
[
