| (1) |
RN/01/14
W. B. Langdon
W.Langdon@cs.ucl.ac.uk
Computer Science,
University College, London,
Gower Street,
London, WC1E 6BT, UK
14 January 2001
Suppose we wish to maximise
subject to the conditions
T>0,
![]() ,
,
![]() and
and
![]() .
.
Since logarithm is a monotonically increasing function for the range of P of interest we can maximise (1) by maximising its logarithm. We do this by differentiating w.r.t. Pi for 1<i<T subject to the constraints. The maximum value of (1) occurs when each of the partial derivatives is zero.
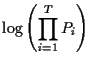 |
= |  |
|
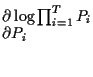 |
= | 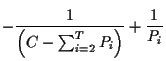 |
Setting each partial derivative to zero
(and noting ![]() )
yields
)
yields
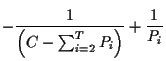 |
= | 0 | |
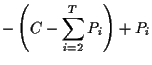 |
= | 0 | |
| -P1 + Pi | = | 0 | |
| Pi | = | P1 |
That is the Pi when (1) is maximal are all equal. Since they still have to sum to C every Pi =1/C.