The computer program performs a
![]() mapping.
Consider the mapping as a truth table with
mapping.
Consider the mapping as a truth table with ![]() rows.
rows.
There are up to
![]() possible tables.
possible tables.
To be reversible, from the output we can infer the input.
Each row in the truth table must be unique.
I.e. the truth table contains a permutation of ![]() numbers.
numbers.
There are only ![]() truth tables (only
truth tables (only ![]() reversible
functions).
Only
reversible
functions).
Only ![]() functions are reversible.
functions are reversible.
Each reversible function can be represented by a number
![]()
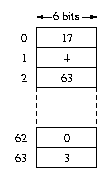
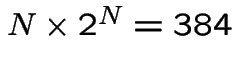 bits
bits
If the set of gates is complete any permutation can be assembled by a suitable sequence of gates.
For simplicity assume there is at least one way of connecting at least one gate so that it does nothing (identity function).
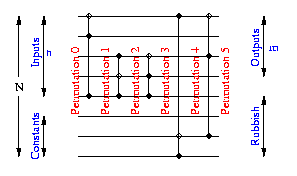
As the program executes (pass through each gate) the state of the
![]() lines changes from one permutation to another.
lines changes from one permutation to another.
Each gate transforms the current permutation to another.
I.e. maps one number in the range
![]() to another.
to another.
Now each gate is reversible. So each output number is uniquely mapped to one input number.
We can represent any reversible gate by a
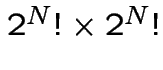 square matrix where each row contains exactly one one,
and each column contains exactly one one
(it is double stochastic).
square matrix where each row contains exactly one one,
and each column contains exactly one one
(it is double stochastic).

At each step (gate) the current permutation is randomly changed. The next permutation depends only on the current one and the randomly chosen gate.
This means the operation of the program is a Markov process whose update matrix is the average of all the gate matrices.
Since the average matrix is:
fully connected all permutations can be reached eventually
acyclic since we have an identity operation
the average matrix has at least one non-zero element on the diagonal
double stochastic
With long programs, all permutations are equally likely [Feller, 1957].