Emergent Behaviour, Population-based Search and Low-pass Filtering
Riccardo Poli,
Alden Wright,
Nic McPhee
W. B. Langdon
Computer Science

Paper presented at CEC-2006
Pages 395-402
Introduction
- Paper covers emergent behaviour in population based search (e.g. PSO and GAs). In some ways we can treat a group as like an individual.
- Mathematically model populations as a hill climber on equivalent smoother landscape (Using genetic program to find equivalent landscape).
- Schema theorem based proof that crossover smoothes landscapes
- Runs on rugged one-mix problem
- Conclusions
Frequency Response for GA
- Present proof for two bits (large pop)
- But result can be generalised for any length bit string, any direction, any (homologous) crossover, at any rate, and with selection.
- Started Walsh analysis to give general frequency response.
Crossover Smoothes Landscape
- Ignore drift by assuming large population.
- n(00) copies of string 00. Two bits, so pop is split between n(00) n(01), n(10) and n(11).
- The average slope in direction x2 is ½|n(11)-n(10)|+½|n(01)-n(00)|
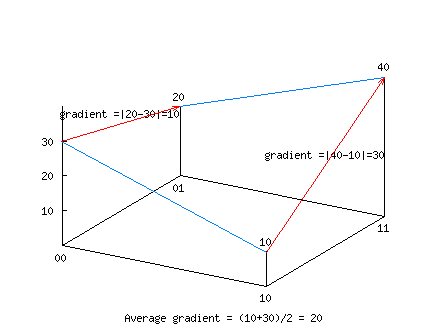
Use Schema Theorem
- 100% one point crossover exact schema theorem says
ní(i,j)=n(i,*)n(*,j)
- Where ní indicates next generation
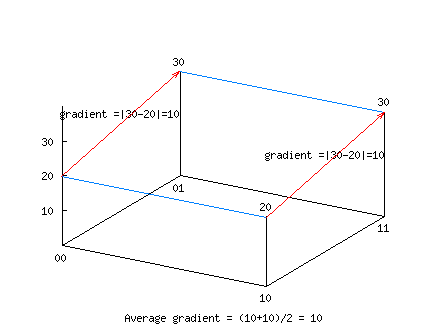
Average Slope in next generation
= ½|ní(11)-ní(10)|+½|ní(01)-ní(00)|
= ½|n(1*)n(*1)-n(*1)n(*0)|+½|n(0*)n(*1)-n(0*)n(*0)|
= ½n(1*)|n(*1)-n(*0)|+½n(0*)|n(*1)-n(*0)|
= ½(n(1*)+n(0*))|n(*1)-n(*0)|
= ½|n(*1)-n(*0)|
= ½|n(11)+n(01)- n(10)-n(00)|
= ½|n(11)-n(10) +n(01)- n(00)|
≤ ½|n(11)-n(10)|+½|n(01)- n(00)|
Steps in Prove
- Average slope in next generation
- Use exact schema theorem on previous gen
- Move common factors outside | |
- Collect in () and | |
- Use n(1*)+n(0*) = n(**) = 1
- Re-express schema in terms of strings
- Re-order
- Use |a+b| ≤ |a|+|b|
Crossover reduces slope
- Prove shows average gradient parallel to second dimension is smaller than it was before crossover.
- |a+b|=|a|+|b| only if sign(a)=sign(b).
- I.e. average slope is same only if two slopes we are averaging are either both up or both down.
- With L bits average over 2L-1 slopes. Unlikely all 2L-1 vectors have the same sign.
Generalisation
- Paper contains proof of extension to
- Any direction parallel to co-ordinates
- Any length bit string
- Any type of crossover
- Any crossover rate
- In fact can also extend to include selection
- Obviously mutation tends to decrease number of popular strings and increase less numerous ones. I.e. to reduce slope
Demonstration: OneMix
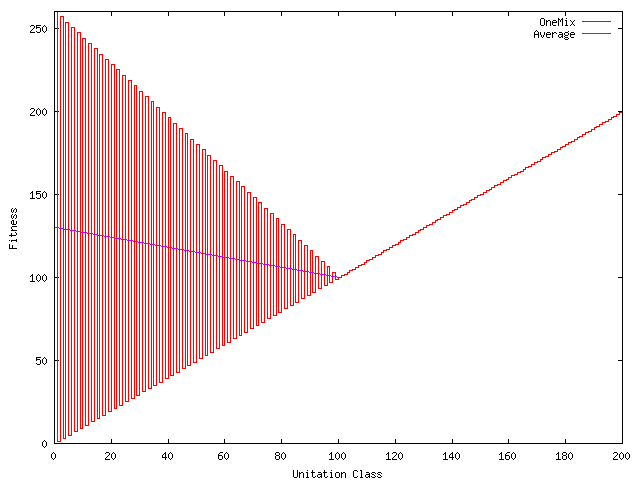
OneMix
- Half of OneMix is identical to OneMax
- But if less than half bits set, fitness varies rapidly with #bits set (i.e. unitation).
- Odd unitation values are still OneMax but if an even #bits set, OneMix like ZeroMax.
- Scaled so optimum is at 000...
- But average fitness near 000... is less than average near 111...
GA and OneMix
- 1/L mutation and uniform crossover, binary tournaments, steady state pop=1000; GA filters landscape and population follows average to 111...
- GA with crossover responds more to low frequencies.
- 1/L mutation and no crossover, binary tournaments, steady state, pop=1000; population steps two bits at a time towards 000...
- GA with only mutation responds more to higher frequencies.
- By tuning balance between selection strength, mutation and crossover rates, the population can be driven to either extreme.
Infinite Population Unitation Model
- Wright+Richter propose an infinite population model. It requires various assumptions but gives exact results with unitation problems of up to 60 bits.
- Plots on OneMix show:
- Selection tries to amplify high frequency components,
- Both mutation and crossover filter but crossover is more effective.
OneMix Infinite Pop g=1 Crossover
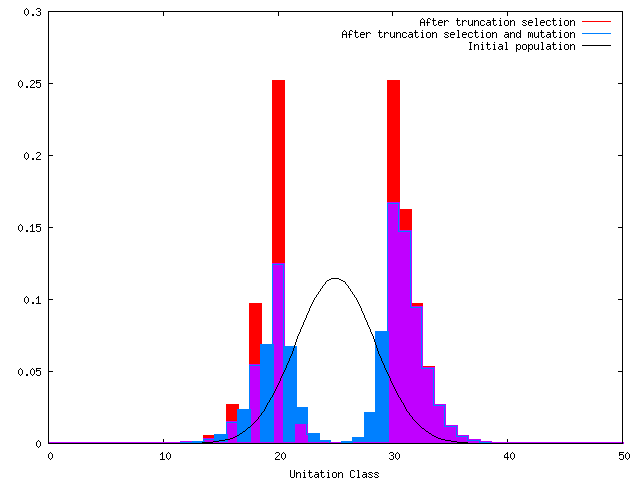
Initial population is Gaussian.
Selection responds to all frequencies.
Crossover responds to low frequencies.
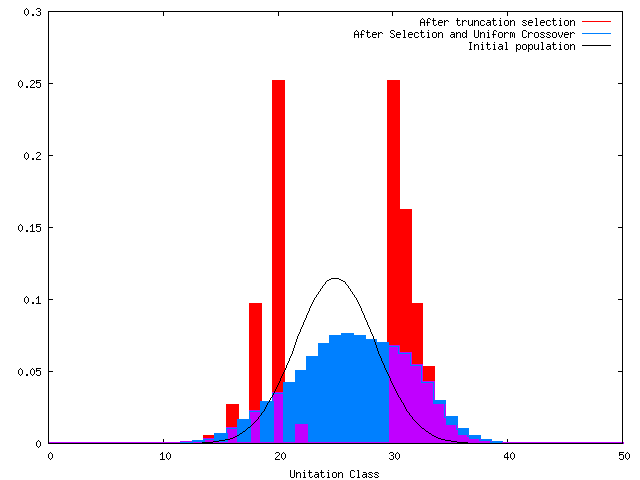
OneMix Infinite Pop g=1 Mutation
Selection responds to all frequencies.
Mutation responds to higher frequencies
Conclusions
- In some ways a GA population behaves like a single individual moving on a transformed landscape.
- Population average moves like a hill climber on a filtered landscape. Can use genetic programming to find a suitable filter.
- Genetic operators (crossover and mutation) reduce gradient in the population, whilst selection tries to increase them.
- OneMix a useful test bed.
W.B.Langdon
25 July 2006






