"Tripled t-test" -- three-group within-subjects data

Analysed with Repeated Measures ANOVA and various Mixed/Multilevel models

Contents

Generate random data, with vague trend

clear; close all; clc;
N = 6;
randn('state', 0);
time1 = 1+randn(N, 1); time2 = 1.2+randn(N, 1); time3 = 1.5+randn(N, 1);
y = [time1 time2 time3]'; plot(y)
y = y(:); Ny = length(y);

Repeated measures ANOVA (Fixed subject effects)

X = [kron(eye(N),ones(3,1)) kron(ones(N,1),[0 0;1 0;0 1])];
figure; imagesc(X)
c2 = [zeros(N,1);1;0];
[t2 df beta] = spm_ancova(X, eye(Ny), y, c2); beta, df, t2
c3 = [zeros(N,1);0;1];
t3 = spm_ancova(X, eye(Ny), y, c3)

beta =

    0.6021
    0.7060
    0.6514
    0.7381
    0.4572
    1.2046
    0.8389
    1.2232


df =

    1.0000   10.0000


t2 =

    1.4007


t3 =

    2.0424

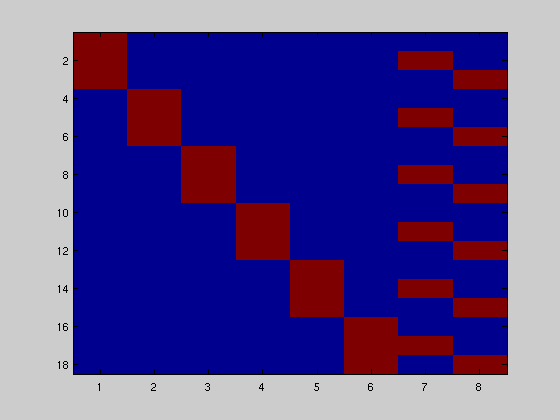
Mixed effects (Equal variances, dependent levels (equal 1-2, 1-3, 2-3)

X = [ones(3*N,1) kron(ones(N,1),[0 0;1 0;0 1])];
figure; imagesc(X)
c2 = [0;1;0];
Q = squeeze(num2cell(zeros(Ny,Ny,Ny),[1 2]));
Q{1} = eye(Ny);
Z = kron(eye(N),ones(3,1)); % design matrix for random subject effects --
% note the similarity to the subject part of X for the fixed model above.
Q{2} = Z*Z'; Nq = 2;
P{1}.X = X;
P{1}.C = Q;
P{1}.W = eye(Ny);
[t df xX xCon beta V C] = spm_reml_ancova(y, P, c2);
E = C{1}.h(1)*P{1}.C{1};
for i=2:Nq
    E = E + C{1}.h(i)*P{1}.C{i};
end
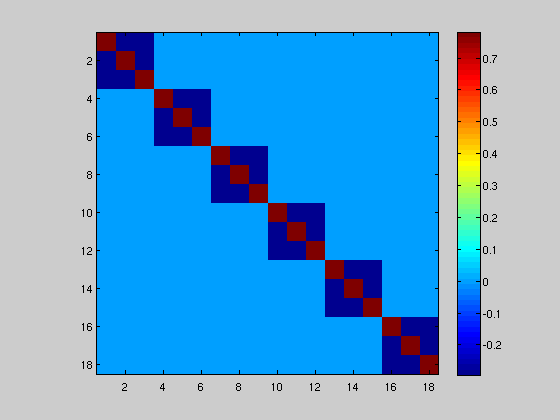
figure; imagesc(E); axis equal; axis image; colorbar
Bcov = inv(X'*inv(E)*X);
beta =  Bcov * X'*inv(E)*y
Bse = sqrt(diag(Bcov));
t = beta ./ Bse

beta =

    0.7266
    0.8389
    1.2232


t =

    2.0126
    1.4007
    2.0424

Multilevel model (Equal variances, dependent levels (unequal deps)

Q = squeeze(num2cell(zeros(Ny,Ny,Ny),[1 2]));
Q{1} = eye(Ny);
Q{2} = kron(eye(N), [0 1 0; 1 0 0; 0 0 0]);
Q{3} = kron(eye(N), [0 0 0; 0 0 1; 0 1 0]);
Q{4} = kron(eye(N), [0 0 1; 0 0 0; 1 0 0]); Nq = 4;
P{1}.X = X;
P{1}.C = Q;
P{1}.W = eye(Ny);
[t df xX xCon beta V C] = spm_reml_ancova(y, P, c2);
E = C{1}.h(1)*P{1}.C{1};
for i=2:Nq
    E = E + C{1}.h(i)*P{1}.C{i};
end
Bcov = inv(X'*inv(E)*X);
beta =  Bcov * X'*inv(E)*y
Bse = sqrt(diag(Bcov));
t = beta ./ Bse

beta =

    0.7266
    0.8389
    1.2232


t =

    2.0805
    1.9849
    1.9525

Multilevel model (SPM's equal var, dept levels: unequal deps as above)

Q = squeeze(num2cell(zeros(Ny,Ny,Ny),[1 2]));
SPM.xVi.I = [kron((1:N)',ones(3,1)) kron(ones(N,1), (1:3)')];
SPM.factor.variance = 0;
SPM.factor.dept = 1;
SPM = spm_get_vc(SPM);
for i=1:length(SPM.xVi.Vi)
    Q{i} = SPM.xVi.Vi{i};
end
P{1}.X = X;
P{1}.C = Q;
P{1}.W = eye(Ny);
[t df xX xCon beta V C] = spm_reml_ancova(y, P, c2);
E = C{1}.h(1)*P{1}.C{1};
for i=2:length(SPM.xVi.Vi)
    E = E + C{1}.h(i)*P{1}.C{i};
end
figure; imagesc(E); axis equal; axis image; colorbar
Bcov = inv(X'*inv(E)*X);
beta =  Bcov * X'*inv(E)*y
Bse = sqrt(diag(Bcov));
t = beta ./ Bse

beta =

    0.7266
    0.8389
    1.2232


t =

    2.0805
    1.9849
    1.9525

Multilevel model (Unequal variances, dependent levels (equal deps))

Q = squeeze(num2cell(zeros(Ny,Ny,Ny),[1 2]));
Q{1} = kron(eye(N), diag([1 0 0]));
Q{2} = kron(eye(N), diag([0 1 0]));
Q{3} = kron(eye(N), diag([0 0 1]));
covs = 1-eye(3);
Q{4} = kron(eye(N), covs); Nq = 2; Nq = 4;
P{1}.X = X;
P{1}.C = Q;
P{1}.W = eye(Ny);
[t df xX xCon beta V C] = spm_reml_ancova(y, P, c2);
E = C{1}.h(1)*P{1}.C{1};
for i=2:Nq
    E = E + C{1}.h(i)*P{1}.C{i};
end
Bcov = inv(X'*inv(E)*X);
beta =  Bcov * X'*inv(E)*y
Bse = sqrt(diag(Bcov));
t = beta ./ Bse

beta =

    0.7266
    0.8389
    1.2232


t =

    1.4676
    1.3344
    1.8388

Multilevel model (Unequal var, dept levels (unequal deps))

Q = squeeze(num2cell(zeros(Ny,Ny,Ny),[1 2]));
Q{1} = kron(eye(N), diag([1 0 0]));
Q{2} = kron(eye(N), diag([0 1 0]));
Q{3} = kron(eye(N), diag([0 0 1]));
Q{4} = kron(eye(N), [0 1 0; 1 0 0; 0 0 0]);
Q{5} = kron(eye(N), [0 0 0; 0 0 1; 0 1 0]);
Q{6} = kron(eye(N), [0 0 1; 0 0 0; 1 0 0]); Nq = 6;
P{1}.X = X;
P{1}.C = Q;
P{1}.W = eye(Ny);
[t df xX xCon beta V C] = spm_reml_ancova(y, P, c2);
E = C{1}.h(1)*P{1}.C{1};
for i=2:Nq
    E = E + C{1}.h(i)*P{1}.C{i};
end
Bcov = inv(X'*inv(E)*X);
beta =  Bcov * X'*inv(E)*y
Bse = sqrt(diag(Bcov));
t = beta ./ Bse

beta =

    0.7266
    0.8389
    1.2232


t =

    1.7215
    2.2910
    1.5801

Multilevel model (SPM's unequal var, dept levels: unequal deps as above)

Q = squeeze(num2cell(zeros(Ny,Ny,Ny),[1 2]));
SPM.xVi.I = [kron((1:N)',ones(3,1)) kron(ones(N,1), (1:3)')];
SPM.factor.variance = 1;
SPM.factor.dept = 1;
SPM = spm_get_vc(SPM);
for i=1:length(SPM.xVi.Vi)
    Q{i} = SPM.xVi.Vi{i};
end
P{1}.X = X;
P{1}.C = Q;
P{1}.W = eye(Ny);
[t df xX xCon beta V C] = spm_reml_ancova(y, P, c2);
E = C{1}.h(1)*P{1}.C{1};
for i=2:length(SPM.xVi.Vi)
    E = E + C{1}.h(i)*P{1}.C{i};
end
figure; imagesc(E); axis equal; axis image; colorbar
Bcov = inv(X'*inv(E)*X);
beta =  Bcov * X'*inv(E)*y
Bse = sqrt(diag(Bcov));
t = beta ./ Bse

beta =

    0.7266
    0.8389
    1.2232


t =

    1.7215
    2.2910
    1.5801

Published with MATLAB® 7.1