one-way, three-level ANOVA (e.g. three groups)

Illustrate tests of "main effect" F-contrast and separate two-sample t-tests (standard, not repeated-measures, ANOVA)

Contents

Data

randn('state', 0);
Na = 10; Nb = 10; Nc = 10; % balanced case
% Na = 10; Nb = 12; Nc = 11; % unbalanced group sizes
a = randn(Na, 1);
b = randn(Nb, 1);
c = randn(Nc, 1);

ANOVA main effect F-contrast

Y = [a;b;c];
X = [ones(size(a)) zeros(size(a)) zeros(size(a))
     zeros(size(b)) ones(size(b)) zeros(size(b))
     zeros(size(c)) zeros(size(c)) ones(size(c))];
Cmain = [1 -1  0
         0  1 -1]';
[Fmain DFmain Bmain] = spm_ancova(X, eye(length(Y)), Y, Cmain)
ResMS = sum((Y-X*(X'*X\X'*Y)).^2)/DFmain(2)
% equivalent alternative F-contrast
Cmain2 = [1    -1/2 -1/2
          -1/2  1   -1/2
          -1/2 -1/2  1  ]';
[Fmain DFmain Bmain] = spm_ancova(X, eye(length(Y)), Y, Cmain)

Fmain =

    0.1588


DFmain =

     2    27


Bmain =

    0.0013
    0.2310
    0.0253


ResMS =

    1.0038


Fmain =

    0.1588


DFmain =

     2    27


Bmain =

    0.0013
    0.2310
    0.0253

Two-sample t-contrasts in ANOVA model

Y = [a;b;c];
X = [ones(size(a)) zeros(size(a)) zeros(size(a))
     zeros(size(b)) ones(size(b)) zeros(size(b))
     zeros(size(c)) zeros(size(c)) ones(size(c))];
Cab = [1;-1;0];
[Tab DFab Bab] = spm_ancova(X, eye(length(Y)), Y, Cab)
Cac = [1;0;-1];
[Tac DFac Bac] = spm_ancova(X, eye(length(Y)), Y, Cac)

Tab =

   -0.5126


DFab =

    1.0000   27.0000


Bab =

    0.0013
    0.2310
    0.0253


Tac =

   -0.0536


DFac =

    1.0000   27.0000


Bac =

    0.0013
    0.2310
    0.0253

Separately modelled two-sample t-tests

Yab = [a;b];
Xab = [ones(size(a)) zeros(size(a))
       zeros(size(b)) ones(size(b))];
Cab = [1;-1];
[Tab DFab Bab] = spm_ancova(Xab, eye(length(Yab)), Yab, Cab)
Yac = [a;c];
Xac = [ones(size(a)) zeros(size(a))
       zeros(size(c)) ones(size(c))];
Cac = [1;-1];
[Tac DFac Bac] = spm_ancova(Xac, eye(length(Yac)), Yac, Cac)

Tab =

   -0.5750


DFab =

    1.0000   18.0000


Bab =

    0.0013
    0.2310


Tac =

   -0.0508


DFac =

    1.0000   18.0000


Bac =

    0.0013
    0.0253

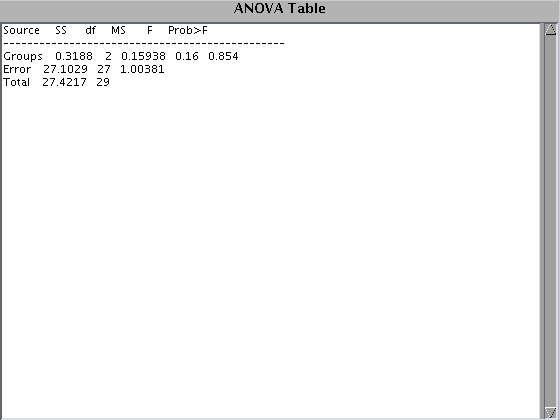
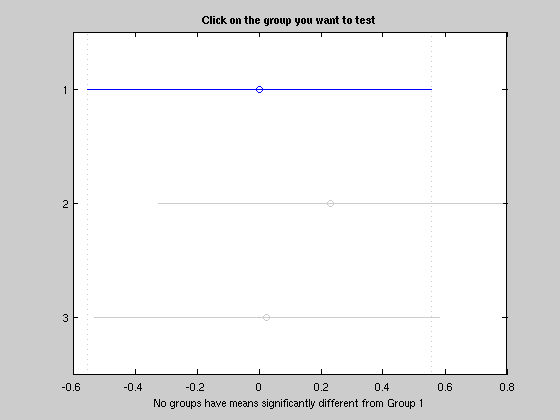
See also anova1 and multcompare in MATLAB

[p tab st] = anova1(Y, [ones(Na,1);2*ones(Nb,1);3*ones(Nb,1)]); st
mc = multcompare(st);
% Note, multcompare uses only the information in the st structure, it
% doesn't perform separate two-sample t-tests. Compare e.g.
Bmain = st.means'
DFmain = st.df
ResMS = st.s^2
% this leads me to believe that the ANOVA approach is correct. Though note
% that the above didn't touch on the multiple comparison adjustment issue.

st = 

    gnames: {3x1 cell}
         n: [10 10 10]
    source: 'anova1'
     means: [0.0013 0.2310 0.0253]
        df: 27
         s: 1.0019


Bmain =

    0.0013
    0.2310
    0.0253


DFmain =

    27


ResMS =

    1.0038

Published with MATLAB® 7.1