Kalman Filter Example
Using Kevin Murphy's toolbox, and based on his aima.m example, as used to generate Figure 17.9 of "Artificial Intelligence: a Modern Approach", Russell and Norvig, 2nd edition, Prentice Hall.
Ged Ridgway, Nov 2006
Contents
Physical system
A point moving in a plane with constant (but noisy) velocity, where only position is observed.
State = (x1 x2 x1dot x2dot) Observation (x1 x2) Unit time-step => xi(k) = xi(k-1) + xidot(k-1) + noise xidot(k) = xidot(k-1) + noise zi(k) = xi(k) + noise
Setup state space model
n = 4; % state size m = 2; % observation size F = [1 0 1 0; 0 1 0 1; 0 0 1 0; 0 0 0 1] H = [1 0 0 0; 0 1 0 0] Q = 0.1*eye(n); % R = 1*eye(m); R = 0.3*eye(m); initx = [1.5 6.5 1 0]'; initV = 10*eye(n);
F =
1 0 1 0
0 1 0 1
0 0 1 0
0 0 0 1
H =
1 0 0 0
0 1 0 0
Sample from state space (linear dynamical) system
seed = 9; rand('state', seed); randn('state', seed); K = 15; [x,z] = sample_lds(F, H, Q, R, initx, K); figure; hold on; axis equal; axis([0 12 0 10]); plot(x(1,:), x(2,:), 'ks-'); plot(z(1,:), z(2,:), 'g*'); xlabel('X1') ylabel('X2') legend('true', 'observed')
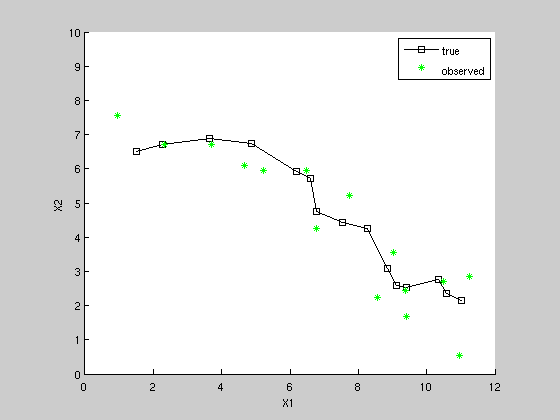
Kalman Filter estimate of state and covariance
(note could use different estimated system, rather than ground truth, e.g. change Q and/or R here -- balance of Q & R has significant effect)
[xfilt, Vfilt] = kalman_filter(z, F, H, Q, R, initx, initV); plot(xfilt(1,:), xfilt(2,:), 'rx:'); for k=1:K, plotgauss2d_old(xfilt(1:2, k), Vfilt(1:2, 1:2, k), 1); end legend('true', 'observed', 'filtered')
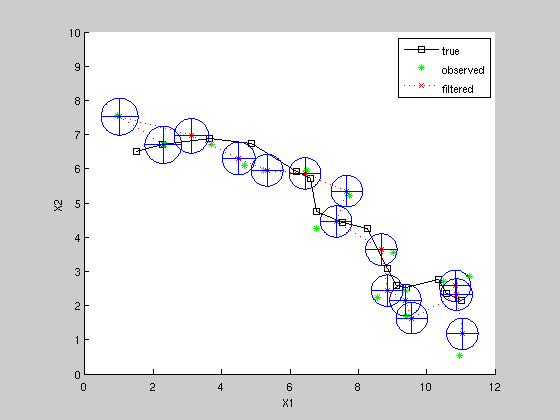
Kalman Smoothing estimate
[xsmooth, Vsmooth] = kalman_smoother(z, F, H, Q, R, initx, initV); figure; hold on; axis equal; axis([0 12 0 10]); plot(x(1,:), x(2,:), 'ks-'); plot(z(1,:), z(2,:), 'g*'); plot(xsmooth(1,:), xsmooth(2,:), 'rx:'); for k=1:K, plotgauss2d_old(xsmooth(1:2, k), Vsmooth(1:2, 1:2, k), 1); end legend('true', 'observed', 'smoothed') xlabel('X1') ylabel('X2')
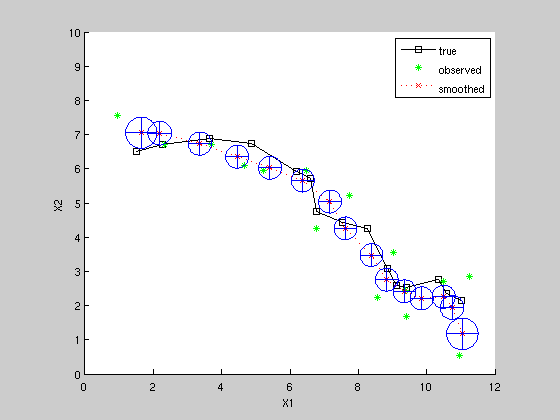
Compare mean squared estimation errors
note smoothing is superior to filtering.
dfilt = x([1 2],:) - xfilt([1 2],:); mse_filt = sqrt(sum(sum(dfilt.^2))) dsmooth = x([1 2],:) - xsmooth([1 2],:); mse_smooth = sqrt(sum(sum(dsmooth.^2)))
mse_filt =
3.0165
mse_smooth =
2.0863