| Computer Science, University College, London |
|
|
| Department of Computer Science, University of Dortmund |
| D-44221 Dortmund |
Is Bloat Due to Introns?
|
|
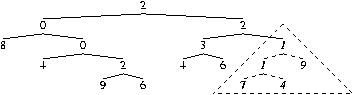
Syntax of tree (i.e. its sequence of functions and leafs) is reduced to hash code.
This is randomised to give a fitness value.
NB fitness depends only on syntax, each tree always has same fitness, many trees share the same fitness value.
If using introns, the whole of subtrees starting with ``1'' are replaced by their first terminal.
So
208042962,34611749 becomes
208042962,3467.
XOR becomes C667BD216 xor D8B16 = C66765916
and randomising yields 4AA4B3316, which has 13 bits set.
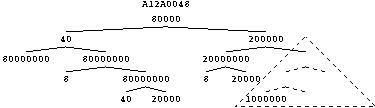
Fitness given by combining ``behaviour'' of every subtree in the program.
``Behaviour'' of whole tree is union of
bits set by each subtree.
Fitness is the number of bits set in the union.
Which bit is set by a subtree is given by calculating is fitness
(using algorithm on page ![[*]](../book.tutorial/cross_ref_motif.gif) -
-![[*]](../book.tutorial/cross_ref_motif.gif) ).
).
Easy - Uniform
Hard - Binomial distribution
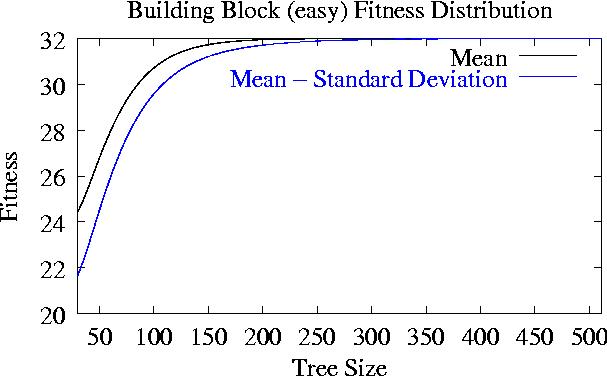
Initially bigger trees have an advantage
but if size
size >200
all same fitness.
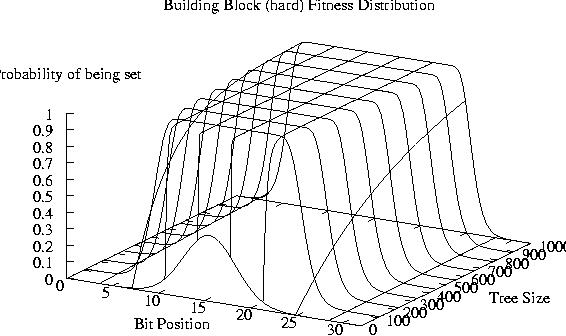
Slow change in distribution w.r.t. size for big trees
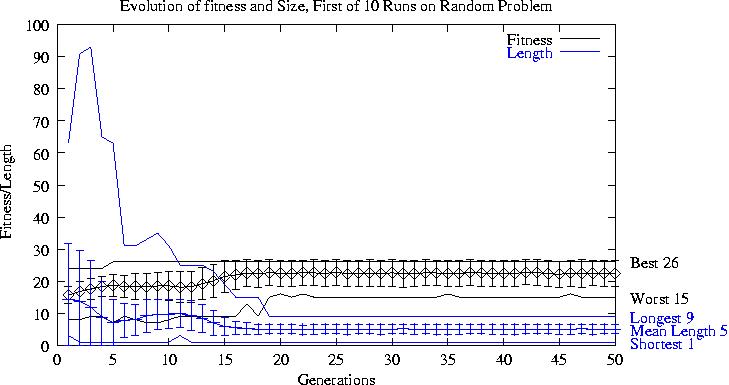
Population quickly reaches a fitness plateau.
Followed by convergence towards a small individual with high fitness.
Stable (1000 generations) populations formed by its children.
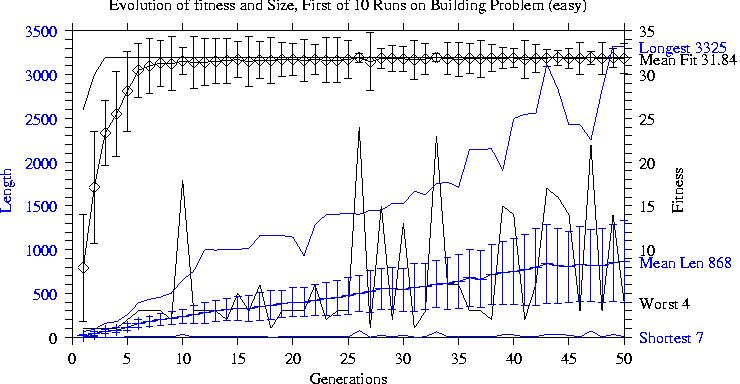
GP rapidly finds trees with maximum fitness.
These spread throughout the population but each generation contains some small low fitness children.
Positive correlation between size and fitness drives increase in size (Price's theorem).
Bloat continues even when most programs in the search space have maximal fitness.
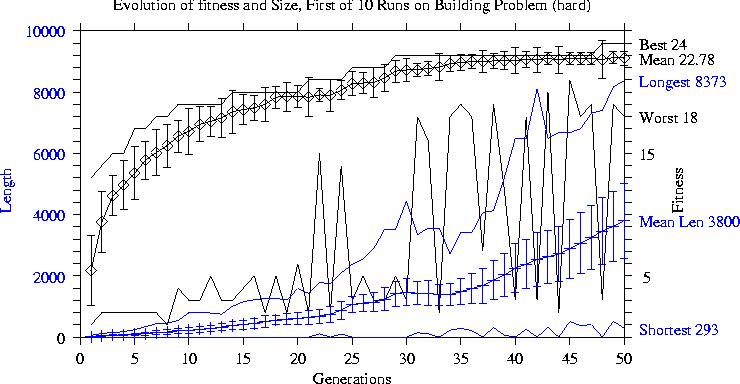
Fitness continues to improve during run but each improvement takes longer to find.
Population converges towards current highest fitness but short and low fitness children are produced in each generation.
Positive correlation between size and fitness drives increase in size.
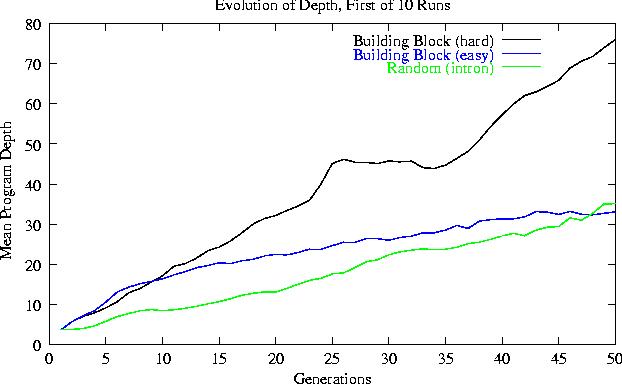
With bushy initial trees, (except for random and easy problems) average program height increases roughly linearly by about one level per generation.
The non-linear, slower depth increase in the easy search spaces is produced by reduced selection pressure.
Other types of initial population increase their depth faster than those starting with bushy trees.
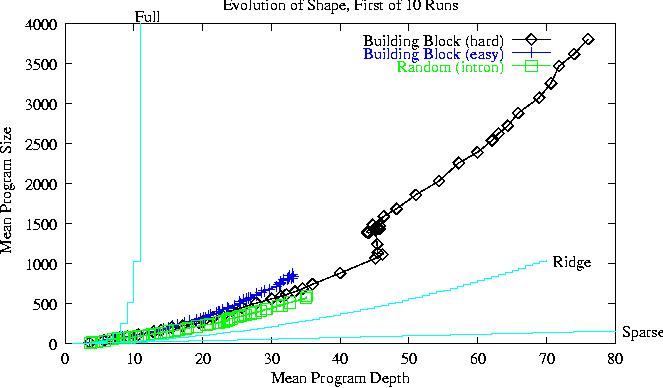
Populations evolve away from the bushy trees created by ``ramped half-and-half'' towards the most popular part of the search space.
| Problem | Final population | Depth | Power law | |||||||
| Fitness | mean size | mean | per gen | Exponent | ||||||
| Random | 25 | (1) | 6 | (0.9) | 3 | |||||
| intron | 25 | (1) | 530 | (200) | 33 | 0.6 | (0.2) | 1.23 | (.09) | |
| BBlock (easy) | 32 | (0) | 870 | (100) | 33 | 0.4 | (0.1) | 1.02 | (.12) | |
| BBlock (hard) | 26 | (.8) | 9000 | (4600) | 132 | 2.8 | (1.7) | 1.34 | (.19) | |
Since programs remain close to the ridge and they increase their depth at a constant rate this leads to sub-quadratic growth in their size.
Linear GP on totally random landscape does not bloat without introns.
Tree GP on totally random landscape does not bloat without introns but is bloat due to introns?
Introduction of correlation (via building blocks or introns) to random landscape and bloat occurs regardless of presence of introns.
Regard bloat as random diffusive expansion of population into available search space. Most of search space is occupied by big random programs (cf. ridge).
GP behaves on these artificial problems like it does on real program spaces (i.e. with semantics).
C++ code may be found in ftp://cs.ucl.ac.uk/wblangdon/gp-code