
William of Occam
William B. Langdon
Computer Science,
University College, London
BNVKI newsletter 19(3) June 2002 pp56-57
Occam, now spelt Ockham, is a sleepy English village in the County of Surrey. Most notable for its village green and quality of its ales but in 1284 it was the birthplace of William of Occam, the famous medieval philosopher and theologian. Who gave us ``Occam's Razor'', Entia non sunt multiplicanda praeter necessitem (Entities must not be multiplied beyond what is necessary). He was excommunication for defying Pope John 22 and died in Germany in 1347, probably before he had managed to persuade the Vatican to lift his punishment and so, according to law, went to Hell.
Occam's Razor, or Occam's Principle,
is often invoked
to justify choosing simpler explanations or theories
over more complex
and to prefer simpler models over more complex ones.
A famous example is the acceptance of Kepler's (1571-1630) Laws
and their
explanation of, and their ability to predict,
the apparent motion of the planets in the night sky.
Kepler's model says
the planets move in ellipses around the Sun, while being viewed from
the Earth, which itself moves along an ellipse about the Sun.
This replaced the earlier notion of the planets, the Sun and the Moon, moving
on concentric circles about the Earth.
To be even slightly predictive the older model had to allow
some planets not to rotate about the Earth
but instead to rotate on other circles
which themselves rotated about the Earth.
The older model was rejected,
especially as further celestial gearing was required to keep
pace with ever more numerous and accurate astronomical data,
including Galileo's discovery in 1610 of moons orbiting Jupiter.

William of Occam
Nearer to home, given two artificial neural networks with similar abilities to model data, we use the simpler network. That is, the network with fewer internal components. While this seems intuitively reasonable, and in keeping with Occam's Razor, it is often justified by the assertion that smaller models generalize to new data better. New mathematical proofs challenge this assumption.
In [Langdon and Poli, 2002] we consider models that can be expressed as computer programs. At first sight this might seem like a restricted set of models, but the opposite is true. Machine learning techniques (such as neural networks) run on computers and the models they generate require a computer program to implement them. In other words, machine learning models are a subset of all the possible programs.
If we consider all the programs that run a certain number steps and then halt, they will implement a certain number of functions. Some functions will be implemented by many programs and others by fewer. That is, we have a distribution of functionality. If we generate a program of the given size at random, its behavior will be drawn from this probability distribution at random.
Consider a very simply example; programs with two Boolean inputs and one Boolean output. There are only 16 possible functions, but each may be generated by many programs. Figure 1 shows the proportion of programs made from 25 NAND gates which implement each function.
If we choose a different number of NAND gates, i.e. a different program size, then we will get a different distribution (Figure 2).
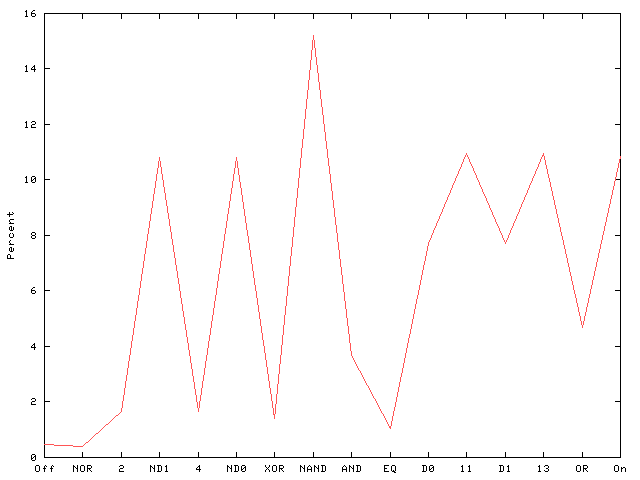
However we have proved for a wide class of programs, as they get bigger their distributions become the same (Figure 3).
Returning to computer models. If we concentrate upon long programs which implement a certain function, e.g. they model some data (such as drug activity) sufficiently well, then we have proved that the chance of creating at random such a program does not vary much with its size. That is, larger models are just as likely to be good as somewhat smaller ones. Furthermore the proof applies to functionality that has not yet been tested. Therefore the chance of creating at random a long computer program that not only models the available data but predicts new data (on which it has not been tested) is also pretty much independent of the model's size. (The probability is of course tiny ) Pragmatically we still prefer small models. For instance, because they consume fewer computer resources. Also practical machine learning techniques have biases which may lead them to produce bigger models with poorer performance.
Note that this directly conflicts with the previously stated justification for using ``Occam's Principle''. The chance of a large model (chosen at random) generalising does not depend on its size. An even bigger model, that fits the available data, is just as likely to be able to predict new unseen data.