Data Fusion by Intelligent Classifier Combination
B F Buxton1, W B Langdon1 and S J Barrett2,
1
Department of Computer Science, University College London,2
Cheminformatics Department,Executive Summary
The use of hybrid intelligent systems in industrial and commercial applications is briefly reviewed. The potential for application of such systems, in particular those that combine results from several constituent classifiers, to problems in drug design is discussed. It is shown that, although there are no general rules as to how a number of classifiers should best be combined, effective combinations can automatically be generated by genetic programming (GP). A robust performance measure based on the area under classifier receiver-operating-characteristic (ROC) curves is used as a fitness measure in order to facilitate evolution of multi-classifier systems that outperform their constituent individual classifiers. The approach is illustrated by application to publicly available Landsat data and to pharmaceutical data of the kind used in one stage of the drug design process.
Introduction
It is a common complaint that, at the beginning of the twenty-first century, we are "drowning in data, but starved of information". The computer-based systems deployed in science, engineering, industry, business, commerce and many other aspects of life such as healthcare, now often produce such a variety of data at such a rate that it precludes human analysis. Prime examples include traditional ‘big’ sciences and engineering such as particle physics and astronomy, new sciences such as cheminformatics and bioinformatics, high-tech systems in space and defence, industrial systems, commercial and business systems in marketing, retail and finance.
When it is clear how the data should be analysed, automation of the analysis by computer is reasonably straightforward, but this is increasingly the exception, even in the traditional areas of science and engineering. Often, in particular in industry, commerce and finance, and in the new sciences of cheminformatics and bioinformatics, the greatest interest is in succinctly summarising data in a meaningful way or in discovering interesting subsets of the data. Such information may be used to make predictions of: market values, trends, customer preferences, credit-worthiness, the time to failure of machinery, etc., or to discover new relationships, principles, and patterns that provide insight and can lead to new ways of working or products. For example in the pharmaceutical industry, it can lead to potential new drugs. The terms ‘data mining’ and ‘knowledge discovery’ have been coined to describe such activities1.
Intelligent systems
Statistical methods are, of course, an indispensable tool for analysing such data and are good at elucidating linear relationships. In addition to such traditional methods, a large variety of "intelligent" techniques such as expert systems, artificial neural networks, fuzzy logic, decision trees, radial basis functions and inductive logic programming have also come into widespread use. Such intelligent systems are not only more general than traditional statistical techniques or operations research methods, they also offer better performance and may frequently be more easily tuned or focused to meet operational requirements such as providing more accurate and more consistent decisions than human experts. Key features contributing to the success of intelligent systems, in particular in business and finance2, are their integration with existing computerised systems, their flexibility, and their abilities to learn, adapt, explain, and discover.
Learning means that such systems can be trained from data and can thereby overcome the limitations and gaps inherent in human capacities and knowledge. Adaptation enables them to monitor and refine their performance as circumstances change, whilst their flexibility enables them to operate robustly when data is incomplete or inconsistent, to generalise effectively from the majority of records scanned, and to make graded decisions. The ability of some intelligent systems to provide models and explanations is important in applications where the decision process, or the new relationships and patterns discovered, have to be made transparent and acceptable to people.
Hybrid intelligent systems
In order to obtain the full benefits of the use of intelligent systems, it is necessary to mix and match them as the application dictates and such techniques are often used in conjunction with each other and with evolutionary computing methods such as genetic algorithms and genetic programming3. Hybrid intelligent systems, in which two or more of these techniques and methods are combined are therefore often particularly effective and can overcome the limitations of individual approaches4. Thus, for example, neural networks can be used to learn the soft decision rules for a fuzzy system, or as pattern matchers in expert systems, and genetic algorithms can be used to find fuzzy membership functions, or to find the weights in neural networks. Such hybrids are known as function-replacing systems, but intelligent techniques may also be used in intercommunicating systems, either sequentially to solve the individual components of a complex problem, or in parallel to pool their results in some final data fusion process. Examples of the former include fuzzy clustering and pre-processing for neural networks and the use of expert systems as ‘seeds’ for genetic algorithms, whilst the latter include multiple co-operating neural networks and expert systems.
Although there have been a number of very successful applications of hybrid intelligent systems, in particular in finance and business areas4, the development of such systems is still relatively new, so the range of tools and development environments available is small in comparison to those for the more established individual techniques such as neural networks, rule induction or expert systems per se. In addition, most organisations have very few staff who have the skill, training, expertise and experience to develop and apply more than one intelligent technique, so applications in finance and commerce have often been implemented by consultants, expert in the use of a variety of intelligent system techniques and familiar with the business domain.
Pharmaceutical applications
This lack of experience and expertise is felt strongly in the pharmaceutical industry, for example in drug discovery, where not only is much of the effort based on new work in cheminformatics and bioinformatics, but an enormous amount of data is available. As a result of automation, advances in research and development, and international collaboration, data is being produced ever faster, in greater detail, and in new ways. Moreover, the available data may be:
Much effort is, of course, expended on the application of intelligent systems techniques to problems in the pharmaceuticals industry, for example to the elucidation of structure-activity relationships or SAR5. However, the nature of the data and, in particular, the lack of knowledge about the structure of the requisite chemical, pharmacologicial and biological problem spaces and how to represent them, mean that these are difficult problems calling for the application of the latest techniques and their incorporation in hybrid intelligent systems. Both were therefore included in the aims of our project on "Intelligent Data Analysis and Fusion Techniques in Pharmaceuticals, Bioprocessing and Process Control" in collaboration with SmithKline Beecham, Glaxo-Wellcome (now GlaxoSmithKline), Unilever, AstraZeneca (now with Syngenta), and SPSS (initially as Integral Solutions Limited), one of the four initial ‘flagship projects’ of the INTErSECT (Intelligent Sensors for Control Technologies) Faraday Partnership managed by NPL and Sira. An example of the former, the application of some of the latest machine learning techniques, in particular, support vector machines (SVM) to the SAR (structure-activity-relationship) problem is discussed in a companion paper. In the remainder of this paper, we shall focus on the development of a hybrid system in which the results obtained from many individual techniques may be combined.
In a pharmacological application, such a system can be used to classify compounds as potentially active or inactive, as described below. Since potential drug compounds can be screened en mass and potential leads are always subject to further investigation before drug development, there is no need in this type of application for the system to be able to offer an explanation of its results. A confidence measure is of course always useful, but the paramount requirement is for accuracy, so that resources are not wasted screening or investigating compounds that turn out to be useless, or opportunities for the development of new products, missed. Similarly, there is no emphasis on the computational speed of a system and little interest in the computer time and resources needed to train it, provided, of course, that these do not become prohibitive. The amount and type of data needed to build the system, in particular to train its constituent classifiers and arrive at the best way to combine them is of interest, however. Even though there is usually a lot of training data available, this is often far from ideal. There thus may, as in many other applications, often be much to be gained from careful preprocessing of the training data, for example to remove inconsistencies, reduce the number of incomplete records, or to make it better balanced.
Classifier fusion
Although we have a fairly specific pharmacological application in mind, the problem is one typical of classifier fusion. The development of multiple classifier systems (MCS) has received increasing attention of late6,7, as it has been realized that such systems can be more robust (i.e. less sensitive to the tuning of their internal parameters, to inaccuracies and other defects in the data) and more accurate than a single classifier alone. In view of the difficulty of the problems encountered in the pharmaceutical industry described above, these are highly desirable properties, but it should be noted that, in general, there is no guarantee that a multiple classifier system will be more robust or more accurate than either the individual classifiers of which it is comprised or than the best single classifier that might otherwise be built7. As frequently occurs in pattern recognition problems where, for example, including irrelevant features often reduces a classifier’s accuracy, "more is not always better".
These caveats notwithstanding, the principle of classifier fusion is simple enough. For example, if we have three systems which may be used to classify a compound as ‘active’ or ‘inactive’ against a particular target, we could take a majority vote and, if the classifiers do not all agree, in the absence of other information indicating the failure or inapplicability of the dissenting classifier on a compound of interest, treat a majority decision as of lower quality than a unanimous one. However, if some classifiers are known to perform better than others in certain regions of the input space, these can be preferentially selected and, in particular if many individual classifiers are available, only the votes of the best classifiers counted. If the individual classifiers deliver only simple binary decisions, this is about as sophisticated as we can be in combining them.
However, if the individual classifiers also produce confidence measures or estimates of the a posteriori probabilities of the output classes, as Bayes classifiers and properly trained feed-forward neural networks do, then there are many other ways in which they can be combined. For example, their outputs can be weighted and summed to produce an average or consensus decision, a combination often known as a "committee". Such a combination is only known to be valid when each of the classifiers contributes little information and the a posteriori probabilities of the output classes are only slightly different from the a priori class probabilities (i.e. little information is gained from the measurements). Nevertheless, it is widely used and seems often to be preferred to other combinations because of its robustness to noise and errors8. In principle, when the classifiers make independent decisions, based for example on distinct input data or they have been trained on different, independent data sets, they should be combined by multiplication of the a posteriori probabilities of the output classes8. Unfortunately, although statistically optimal, this combination is sensitive to errors and, in particular, a single zero (or very low) output probability can dominate the decision in what is known as a ‘veto’ effect.
Classifier combination strategies
Since the best combination of a set of classifiers depends on the application and on the classifiers to be combined, there is no single, best combination scheme nor any unequivocal relationship between the accuracy of a multiple classifier system and the individual constituent classifiers9. One approach is to generate a large number of classifiers and then to select the best combinations to use in particular regions of the input space. This raises two questions: first, how to generate a suitable set of classifiers, and then how best to combine them. Although these questions should, of course, be considered simultaneously, they are often treated separately as coverage optimisation and decision optimisation strategies10. In coverage optimisation, the combination rule is fixed, for example as a majority vote or as a weighted average. Effort is then concentrated on generating complementary classifiers whose errors are, as far as possible, uncorrelated. One way is to select random subsets of the measured features as inputs to different classifiers. Another is to train classifiers on different data sets. The latter is used in ‘boosting’ methods11 which, as discussion of the additive combination rules above suggests, work best if the individual classifiers are ‘weak’.
Alternatively, if a number of classifiers, such as neural networks of different architectures, naïve Bayes classifiers, SVMs with different kernel functions, decision trees etc, are available, the question arises as to how best to combine them. Since, even in a selective voting scheme, n classifiers may be combined in 2n ways, it is difficult to carry out exhaustive experiments except in simple or restricted circumstances9. Several search techniques have been used, including forward and backward search, tabu search, and genetic algorithms12, 13, 14 to find the best multiple voting scheme, but these address only one way of combining classifiers. A more powerful technique capable of finding an arbitrary combination function is needed in general.
Genetic programming
Fortunately, there is such a technique, known as genetic programming15 or GP for short. Essentially, it uses a genetic algorithm or other evolutionary strategy16 to evolve a program that, for example, solves a problem characterised by training data obtained from known examples. In our case, the program evolved tells us how to combine the classifiers. GP automatically specifies the combination function and implements it. The technique may be regarded as an intelligent search method that manipulates a population of potential solutions both to focus on parts of the search space likely to contain the best solutions and to avoid becoming trapped in poor, local optima. In general, GP works by building a population of potential programs from a collection of elementary functions such as: add, subtract, multiply, a protected divide (which does not diverge on division by zero) max, min, etc, plus a number of constants usually initially chosen at random. The programs evolved are encoded as a tree structure, which is sufficiently powerful to represent any program and facilitates substitution of an evolved sub-tree or useful procedure into other nodes of the tree. Complex programs may therefore be created in a small number of steps or ‘generations’.
The programs created are controlled by the fitness function ascribed to each member of the population, the evolutionary strategy such as the selection mechanism, and the evolutionary parameters chosen such as: mutation rate, cross-over rate, and number of generations, etc. ‘Shrink’ and ‘sub-tree’ parameters17 are used to help prevent very large program trees from being produced, but even so, the functions produced by a genetic program are often quite complicated. Like the structure of a typical neural network, the programs evolved are thus not usually easy to interpret or understand in detail. However, in applications where accuracy is the main concern and the system is used as a ‘black-box’, these are unimportant factors. In any case, if desired, as for example in finance applications, additional fitness components may be included in order to produce simple programs, representing simple combination rules that can be explained in a few sentences of English18.
The ROC curve and Wilcoxon statistic
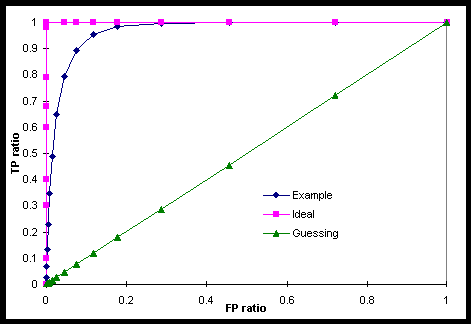
The choice of fitness function is very important as it strongly affects the programs evolved. We want to evolve a combination of classifiers that is as accurate as possible and, in particular, one that classifies few useless compounds as active (false positives) and misses few potential leads for new drug development (false negatives). Whilst the cost of the former could be evaluated, the latter is very hard to assess. It is thus difficult to tune the classifier system optimally to trade-off one type of error against the other. A more robust performance criterion is required that is not dependent on such detailed knowledge. Fortunately, such a criterion is available if, instead of producing a single classifier, we construct classifiers whose decisions can be tuned by varying a threshold. For example in our pharmaceutical application, at a low threshold every compound might be classified as active by such a classifier, implying a true positive rate (TPR) of one (100%) but also a false positive rate (FPR) of one, whilst at a high threshold everything might be classified as inactive, giving a false positive rate of zero but also a true positive rate of zero. Obviously such outcomes are not useful, but as the threshold is varied, the system’s performance can be tuned between these extremes along its receiver-operating-characteristic (ROC) curve.
An example for the case where the class distributions are both Gaussian is illustrated in Figure 1. The figure shows that good performance with TPRs close to one and simultaneously small FPRs can be achieved. However, since the tails of the class distributions overlap, the ideal of a TPR=1 with a FPR=0 (in the top left corner) is unattainable. The diagonal straight line in Figure 1 is what would be obtained by biased random guessing from one extreme in which every compound was assumed inactive at (0,0) to the other extreme where every compound is assumed active at (1,1). The closer the ROC curve comes to the top left corner where TPR=1 and FPR=0, the better. The area under the curve, which can be at most one, thus suggests itself as a good, robust performance measure. In fact, it follows from the properties of such a decision system that the area under the ROC curve is the Wilcoxon statistic. This is a precise statistical measure of performance based on the frequency with which (in this application) the system correctly ranks the activity of interesting compounds in comparison to the activity of uninteresting compounds. Because the Wilcoxon statistic is independent of the class distributions and, given a set of training examples, is easily estimated from the area under an ROC curve, it is a robust and convenient measure of performance. It is frequently used in the design of medical systems and procedures19 where the cost of a false negative outcome in which a diseased patient is declared healthy can also be very difficult to quantify.
Combined classifiers and the MRROC
In order to use the area under the ROC curve as a fitness function in the GP, we need to consider what happens when classifiers are combined. This is illustrated in Figure 2, constructed for an example from Scott et al20 in which the class distributions are bimodal. The individual classifiers do not perform well, in particular between points the marked 4 and 8. We can do better by choosing between the results delivered by the classifiers at the points marked 4 and 8 in a manner analogous to the random guessing on the straight line in Figure 1. By this means, the performance of the composite classifier can be set to any point on the convex hull of the ROC curves of the individual classifiers. This is a general prescription20, known as the ‘maximum realizable ROC’ or MRROC for short. Although we can always construct the MRROC, it is possible, both in principle and in practice to do better.
Our GP thus works as follows. Given the individual classifiers and how they perform on a training set of examples, it searches for combinations of the classifiers whose performance lies outside the MRROC of the constituent classifiers. Both the outputs and confidences of the classifiers are required at a range of operating thresholds to do this. When such combinations are found, an ROC is constructed from their convex hull and, if required, the ROC of the individual classifiers. The area under this convex hull is necessarily greater than the area under the MRROC, leading to a better multiple classifier system. Since the search space can be very complicated there is, however, no guarantee of improvement and the number of possible combination functions is very large. A powerful search technique such as genetic programming, which also has the flexibility to represent arbitrary functions, is therefore required.
Examples
Details of the method, which has been tested on several examples from the literature, are given in a number of recent publications21, 22, 23. The examples tested include those benchmarked by Scott et al20 and, in every case, the GP evolved a superior combined classifier. Here we quote the results from one23, in which three types of classifier: a neural network, naïve Bayes, and a C4.5 decision tree were used on a Landsat dataset in the UCI machine learning repository to classify pixels as in Scott et al20. In order to ensure complementarity, each type of classifier was trained on data from one spectral band23. Results on holdout data, none of which was used to train the individual classifiers or to evolve the multiple classifier system, are shown in Figure 3. All multiple classifier systems produced by the genetic programming perform better than their constituent classifiers. The combined systems thus seem to be robust and capable of generalizing well over unseen data with no evidence of over fitting. Since there is always danger of over fitting, care was taken to ensure that the individual classifiers did not over fit the training data and similarly the parameters and strategy of the genetic program chosen so that it did not over fit in evolving the multiple classifier systems23.
It must be remembered that these results are specific to this particular application and that no general guarantees can be given for the performance of multiple classifier systems. Nevertheless, the approach seems very promising and has led to good combined classifiers on all the examples to studied date21, 22, 23. We have therefore begun further evaluation of the technique on a number of problems in pharmaceutical applications. Preliminary results from one such test on ‘p450’ data supplied by GlaxoSmithKline are illustrated in Figure 4. Sixty neural networks were produced by GlaxoSmithKline using the commercial data mining tool, Clementine, twenty-one of which were automatically selected and combined to give the multiple classifier system shown. Although the multiple classifier system outperforms its constituents, the improvement is not very great and there is, as the small difference between the ROC curves on the training and verification datasets suggests, a slight possibility of over fitting by the genetic program. The lack of dramatic improvement may be because the neural networks used were not complementary enough. Work is therefore in progress to include other types of classifier, such as decision trees that are easily produced by use of commercial tools. In due course, we intend also to incorporate more sophisticated classifiers such as the support vector machines whose application to pharmaceutical problems is described in the companion paper.
Conclusions and future development
It has been described how it can be beneficial, when dealing with difficult data mining problems, for example in the pharmaceutical industry, to combine the results of a number of different classifiers in a hybrid intelligent system. Although there is no general, universally applicable rule as to how classifiers should best be combined, it has been shown that, when the individual classifiers are tunable over a range of decision thresholds and capable of delivering a confidence estimate with their output, genetic programming is a useful tool for evolving appropriate combination functions. An essential ingredient is use of a robust fitness function based on a rigorous measure of classifier performance obtained from the area beneath the convex hull of the ROC. In addition, care was taken, both in producing the individual classifiers and in the design of the genetic program to avoid over fitting. The technique was illustrated by producing combined classifiers for a publicly available Landsat example and for a pharmaceutical problem.
Acknowledgement
This work was carried with the support of the EPSRC via grant, GR/M 43975 under the INTErSECT Faraday Partnership. The authors wish also to acknowledge, on behalf of the project, the support and assistance of their collaborators mentioned in the text and of the Sira-UCL Postgraduate Training Partnership. The Data Mining tool Clementine was provided by SPSS as part of the Faraday project.
References
1. Fayyad UM, Piatetsky-Shapiro G, & Smyth P, From Data Mining to Knowledge Discovery: An Overview, in Advances in Knowledge Discovery and Data Mining, edited by Fayyad UM, Piatetsky-Shapiro G, Smyth P, &Uthurusamy R, AAAI Press/MIT Press 1996, pp. 1-34.
2 S Goonatilake and P Treleaven, (Eds): Intelligent Systems for Finance and Business, John Wiley and Sons, 1995.
3 W B Langdon, Genetic Programming and Data Structures: Genetic Programming + Data Structures = Automatic Programming!, Kluwer, Boston, 1998.
4 S Goonatilake and S Khebbal, (Eds): Intelligent Hybrid Systems, John Wiley and Sons, 1995.
5 Hansch C & Leo A: Exploring QSAR Fundamentals and Applications in Chemistry and Biology, vols1 & 2, ACS, Washington DC, 1995.
6 Kittler J & Roli F (editors): Multiple Classifier Systems, Proc. of 1st International Workshop, MCS2000, Cagliari, Italy, 21-23 June 2000, Lecture Notes in Computer Science, vol 1857, Springer-Verlag, Berlin.
7 Kittler J & Roli F (editors): Multiple Classifier Systems, Proc. of 2nd International Workshop, MCS2001, Cambridge, UK, 2-4 July 2001, Lecture Notes in Computer Science, vol 2096, Springer-Verlag, Berlin.
8 Kittler J, Hatel JM, Duin RPW, & Matas J: On combining classifiers, IEEE PAMI, 20(3), 1998, pp. 226-239.
9 Kuncheva LI & Whitaker CJ: Feature Subsets for Classifier Combination: An Enumerative Experiment, in ref 7, pp. 229-236.
10 Ho TK: Data Complexity Analysis for Classifier Combination, in ref 7, pp. 53-67, 2001.
11 Freund Y & Schapire RE: Experiments with a new boosting algorithm, in Proc. 13th International Conference on machine Learning, Bari, Italy, 1996, pp. 148-156.
12 Roli F, Giacinto G & Vernazza G: Methods for Designing Multiple Classifier Systems, in ref in 7, pp. 78-87.
13 Sirlantzis K, Fairhurst MJ & Hoque MS: Genetic Algorithms for Multi-classifier System Configuration: A Case Study in Character Recognition, in ref 7, pp. 99-108.
14 Ruta D & Gabrys B: Application of the Evolutionary Algorithms for Classifier Selection in Multiple Classifier Systems with Majority Voting, in ref 7, pp. 399-408.
15 Koza JR: Genetic Programming: On the Programming of Computers by Means of Natural Selection, MIT Press, Cambridge, MA, 1992.
16 Michalewicz Z: Genetic Algorithms + Data Structures = Evolution Programs, 3rd edition, Springer-Verlag, Berlin, 1996.
17 Langdon WB: Size fair and homologous tree genetic programming crossovers, Genetic Programming and Evolvable Machines, 1(1/2), April 2000, pp. 95-119.
18 Bentley PJ: Evolving Fuzzy Detectives: An Investigation into the Evolution of Fuzzy Rules, a late-breaking paper in GECCO '99, July 14-17, 1999,Orlando, Florida USA, pp. 38-47.
19 Swets JA, Dawes RM & Monahan J: Better decisions through science, Scientific American, October 2000, pp. 70-75.
20 Scott MJJ, Niranjan M and Praeger RW: Realisable classifiers: Improving operating performance on variable cost problems, in Proc. of 9th British Machine Vision Conf, Southampton, 14-17 Sept 1998, edited by Lewis PH & Nixon MS, vol 1, pp.305-315.
21 Langdon WB & Buxton BF: Evolving Receiver Operating Characteristics for Data Fusion, in Proc. of EuroGP’2001, Lake Como, Italy, 18-20 April 2001 edited by Miller J et al, Springer Verlag, pp. 87-96.
22 Langdon WB &Buxton BF: Genetic programming for combining classifiers, in Proc. of GECCO’2001, San Francisco, 7-11 July 2001, Morgan Kaufmann, pp. 66-73
23 Langdon WB & Buxton BF: Genetic Programming for Improved Receiver Operating Characteristics, in ref 7, pp. 68-77.
Figures

Figure 1: Example ROC curve for a system described by univariate normal distributions, the straight line obtained by guessing the class membership, and the unobtainable ‘ ideal’ ROC curve.
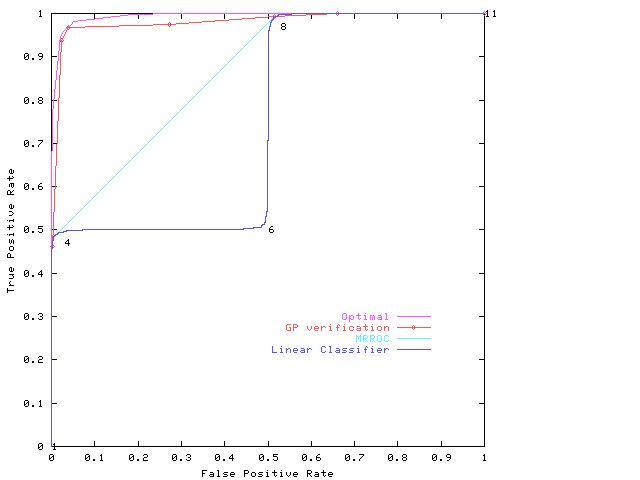
Figure 2: Construction of the MRROC by choosing appropriately between the constituent classifiers at points marked 4 and 8 so as to generate the convex hull of the ROC curves of the two individual classifiers. (Figure 2 accidentally omitted from printed version).
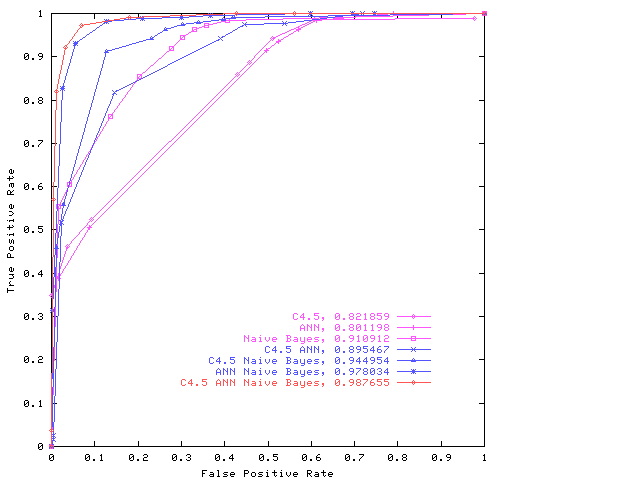
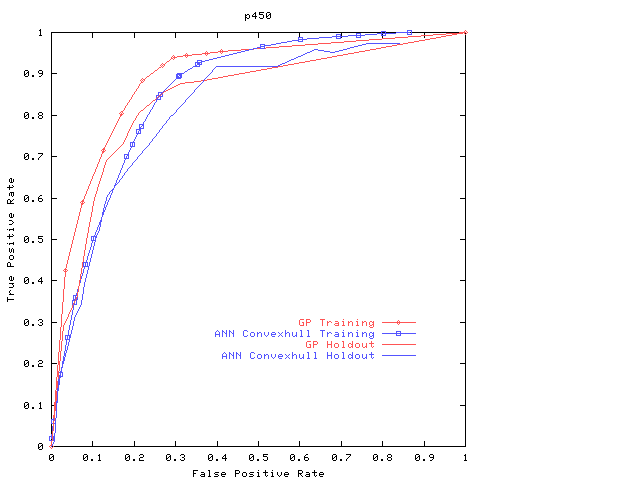
Figure 4: Preliminary results on the pharmaceutical data. Note that the ROC obtained with the multiple classifier system on the holdout data does not have to be convex.