Computer Science

Paper presented at EuroGP-2006
pages 225-237
details

Paper presented at EuroGP-2006
pages 225-237
details
 GP and data structures
evolves GP trees with memory and includes examples of
evolving loops.
GP and data structures
evolves GP trees with memory and includes examples of
evolving loops.

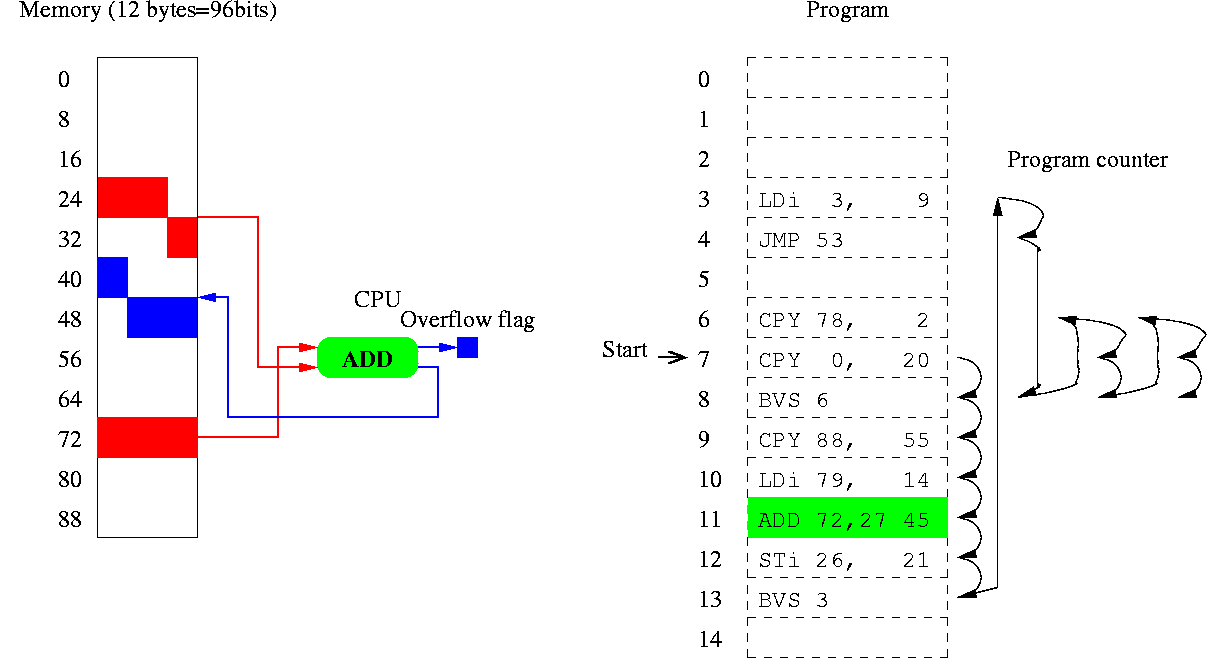
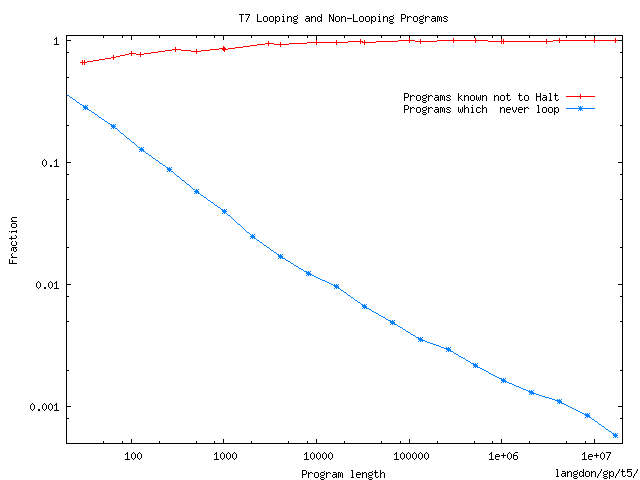
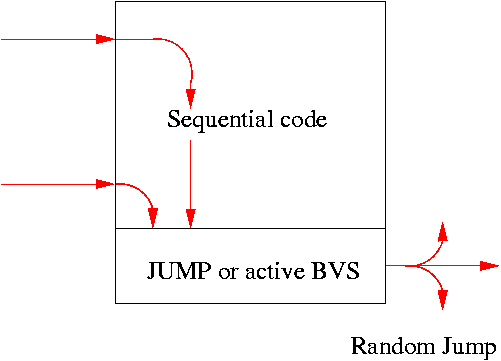
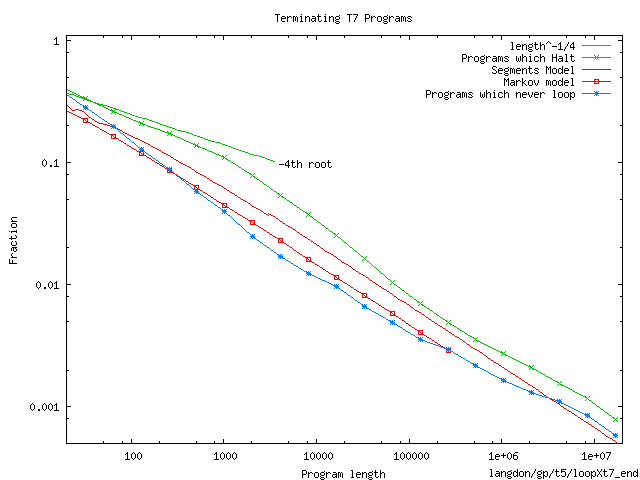
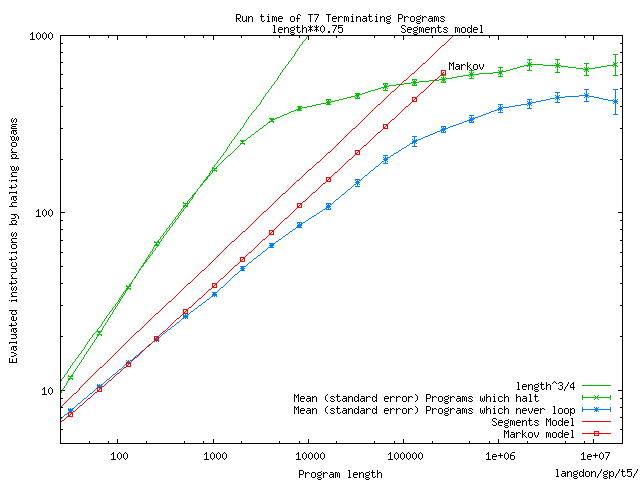
 The number of halting T7 programs containing 16 million instructions exceeds
10100 000 000.
The number of halting T7 programs containing 16 million instructions exceeds
10100 000 000.