Next: About this document ...
Code Growth in GP and other Stochastic Search Techniques
W. B. Langdon
SEN 4
C
ENTRUM VOOR W
ISKUNDE EN I
NFORMATICA,
K
RUISLAAN 413, NL-1098 SJ A
MSTERDAM,

Introduction
- Background
- What is known about the space of all programs
- What is (wrongly?) assumed
- New measurements and conjectures about programs spaces
- Random walk, maximising entropy, model of bloat
- Evolution of shape
- Bloat free operations
Background - Genetic Programming
- Genetic Programming is a stochastic technique that produces programs,
not by constructing them but by using a genetic algorithm to search the
space of possible programs for one of adequate performance.
- In standard GP programs are represented by trees
(cf. lisp S-expressions)
rather than as lines of code. For example, the simple
expression
max(x * x, x + 3 * y);
would be
represented as:
Background - Program Growth in GP
- Surprising programs in GP populations tend to get bigger
- This bloat is widely reported and appears, in the absence of bias, to
be a general feature of GP.
Sextic Polynomial, Best of Initial Population

Ramped-half-and-half (2:6)
Length 11, Depth 4, Fitness 0.043511, Hits 6, constant value,
First run
Sextic Polynomial, First Solution
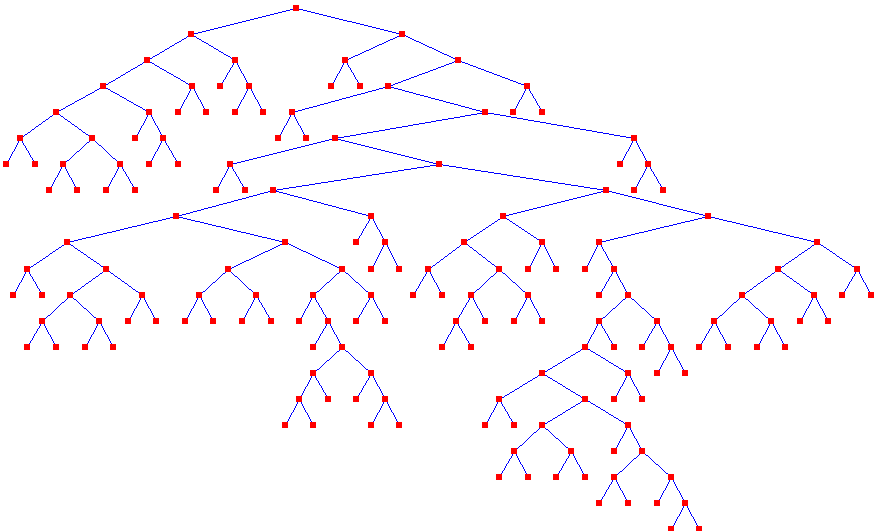
Length 173, Depth 21, Fitness 0.00432659, Hits 50,
generation 37
Sextic Polynomial, Best of Pop, End of run

Length 383, Depth 24, Fitness 0.0029695, Hits 50
Program Growth in GP
- This research grew out of studies of bloat in GP
- Investigate the space GP is searching rather than GP
- Starting from what is known,
I present measurements of spaces from a few benchmark problems,
make a wild claim
(which can be proved in some very special cases)
which challenges the usual assumptions about programs
- We use this to build a model of bloat which is not specific to GP
- This increasing entropy model also predicts program shape
- Present bloat reducing mutation and crossover operations.
What is known about space of all programs
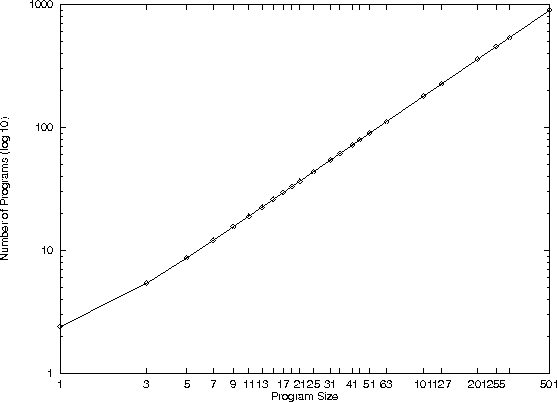
- It is big, graph
-
Program space contains trees of many shapes.
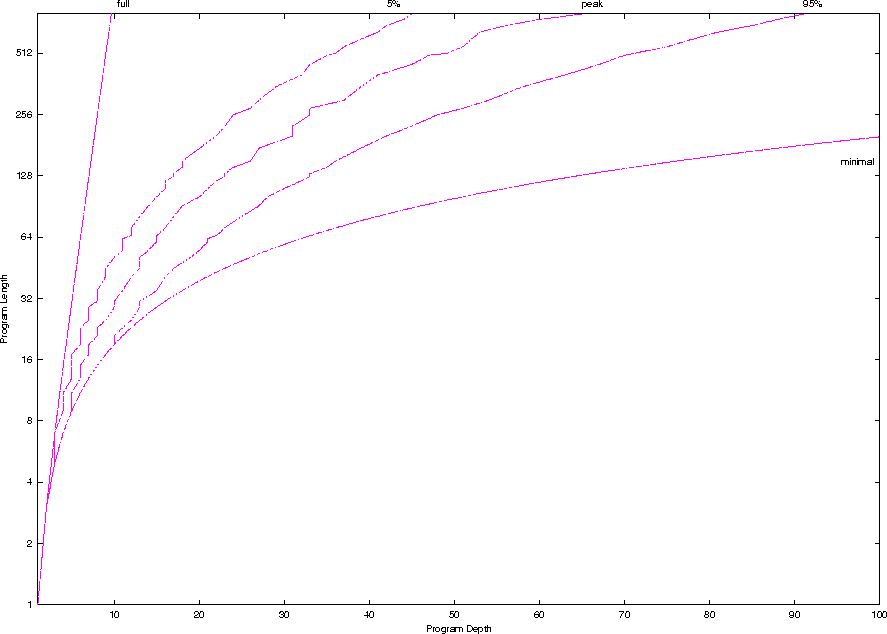
- graph of size v. depth
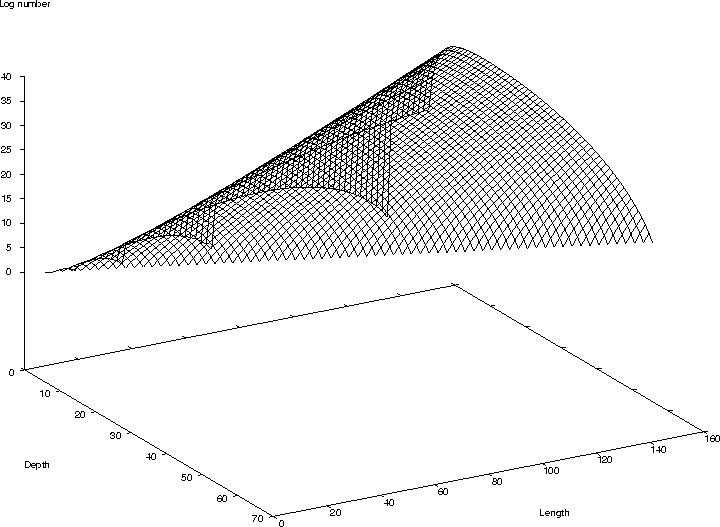
- graph of size v. depth v. number of programs
Number of programs v. size, Sextic Polynomial
Distribution of Binary Trees by size and height
Distribution of Binary Trees by size and height
What is wrongly assumed about space of all programs
- It is widely assumed that programs are fragile
- I.e. any small change will seriously worsen their performance
- I.e. the program landscape is very rugged
- This may not be true.
It is well known that commercial software contains many bugs.
I.e. many small changes exist (bug fixes) which when made only change
the program's performance marginally (make it slightly better).
New measurements and conjectures about programs spaces
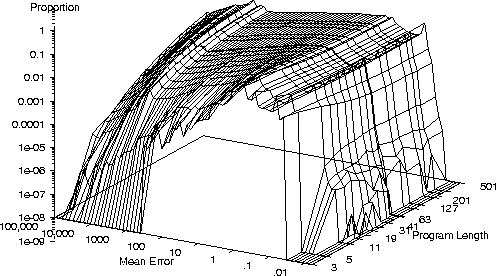
- We measure the fitness of a huge number of programs sampled at random.
- As expected we get a large number of very poor programs and a
tiny fraction of good ones.
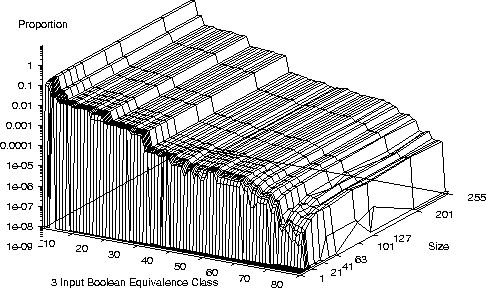
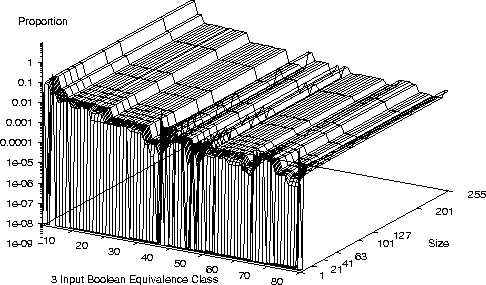
- On a small number of bench mark problems we see
another common characteristic
- Once a, problem dependent, threshold is exceeded program performance
changes only slowly with program length.
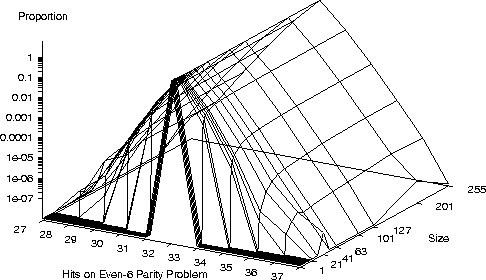
- In the case of the Boolean even-n parity problems using XOR
as the only internal node, this limiting behaviour can be proved.
- graphs of ant problem, all 3 input Booleans (with and without XOR),
6 even parity and 6 always-on (with and without XOR),
Sextic Polynomial.
- counter examples, ant, parity with full trees.
Proportion of Ant programs with each score
Error Distribution Sextic Polynomial Problem
Distribution of 3 bit Boolean Functions
Distribution of 3 bit Boolean Functions with XOR
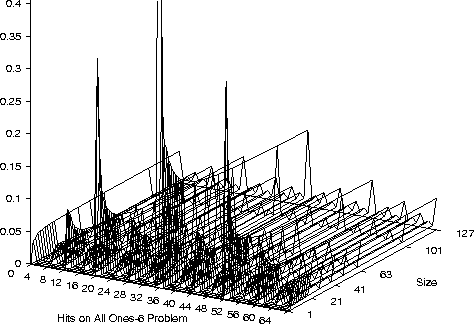
Hits on 6 Inputs All-1s Problem
Even-6 parity program space
Hits on 6 Inputs All-1s,
XOR included
Even-6 parity program space,
including XOR
Implications
- Estimates of density of solutions
- No advantage for uniform random search in looking at long programs
Two Mechanisms for Bloat
- 1.
- Longer programs are more resilient to change.
They are more likely to produce children as fit as they are.
- 2.
- Small changes to existing code is less likely to disrupt it.
However there is no counterbalancing size effect on adding code.
So fit children either result from small removals of code
and small additions or
small removals and large additions.
Together this means fit children are on average bigger than their parents.
Random Walk, Maximising Entropy Model of Bloat
One general cause, although counter examples can be constructed
- 1.
- Practical search techniques start with short candidate solutions
- 2.
- they search the neighbourhood of good solutions
- 3.
- It is easy to make improvements initially
- 4.
- As the best-so-far improves, further improvements become harder
- 5.
- I.e. they get stuck and may execute a random walk amongst
solutions as good as those they have found so far.
- 6.
- There are many more (exponentially more) long programs of this fitness
than short ones.
- 7.
- Thus a random walk is over time far more likely to
increase program size than decrease it.
Bloat is inherent in variable length search
not just GP.
Predications
- Mechanism 1 suggests bloat arises because longer programs are stable.
But may get bloat even
- if kill all stable children
- Change test function every generation
- Can remove second cause by correlating
inserted code size with removed code size
Evolution of shape
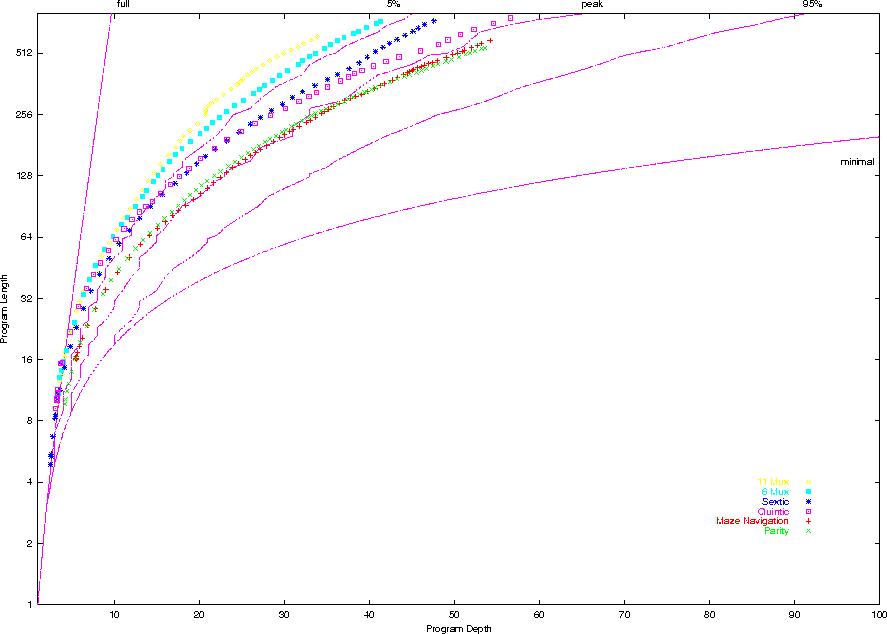
- Maximum Entropy explanation predicts programs will evolve
towards the most common shape with an accessible level of performance.
- plot, shape frequency, Even Parity, Maze, Sextic Polynomial,
Quintic Polynomial, 6 Multiplexor and 11 Multiplexor
Evolution of Shape: 6 Problems
Conclusions
- Claim,
in general,
fitness distributions show little variation w.r.t. program length
once a problem dependent threshold is exceeded.
- The evolution of program size and shape can be explained by
a maximising entropy principle.
- By careful control of the neighbourhoods associated with
genetic operators we can effectively control bloat.
- But in the long term
we can expect in the absence of bias
entropy to a find a mechanism around such controls.
Bloat, Fair v. Standard Crossover
Evolution of shape, Fair v. Standard Crossover



Next: About this document ...
Bill Langdon
1999-03-03



 Ramped-half-and-half (2:6)
Length 11, Depth 4, Fitness 0.043511, Hits 6, constant value,
First run
Ramped-half-and-half (2:6)
Length 11, Depth 4, Fitness 0.043511, Hits 6, constant value,
First run
 Length 173, Depth 21, Fitness 0.00432659, Hits 50,
generation 37
Length 173, Depth 21, Fitness 0.00432659, Hits 50,
generation 37
 Length 383, Depth 24, Fitness 0.0029695, Hits 50
Length 383, Depth 24, Fitness 0.0029695, Hits 50