
University College, London
Genetic Programming and Data Structures, Kluwer, 1998. W.B.Langdon@cs.ucl.ac.uk http://www.cs.ucl.ac.uk/staff/W.Langdon
W. B. Langdon

Genetic Programming and Data Structures, Kluwer, 1998. W.B.Langdon@cs.ucl.ac.uk http://www.cs.ucl.ac.uk/staff/W.Langdon
3.7, 3.8 Come back to as needed
Chapter 8, Price's and Fishers' theorem. GP deception.
Glossary (B),
Scheduling preventive maintenance (C),
Implementation,
caching and speedups,
bench marks,
ftp addresses (D)
![[*]](cross_ref_motif.gif)
| Algorithms + Data Structures | = | Programs |
| Genetic Algorithms + Data Structures | = | Evolution Programs |
| Genetic Programming + Data Structures | = | Automatic Programming! |
``To build [or evolve] a successful program, appropriate data structures should be used together with appropriate algorithms (these correspond to genetic operators used for transforming individual chromosomes [or programs])'',
[Michalewicz1994, page xi].
One memory cell M0, function SETM0 and terminal M0 (reads M0) [Koza1992]
What to do if M0 is not set?

32 bit integers. Strongly Typed Genetic Programming (STGP)? [Montana1995]
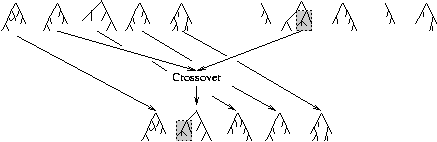
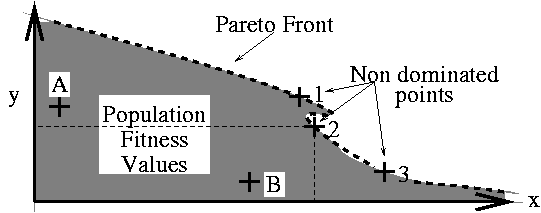
and better in at least one dimension then it dominates
As
![]() but
but
![]() ,
,

individuals are preferred if there are few others that dominate them.
(user to define which?)

Generated at random (but don't pop empty stack)
different proportion of operations in each sequence.
memory reset before each sequence
| Test Sequence | makenull | top | pop | push | empty | Totals |
| 1 | 2 | 2 | 14 | 14 | 8 | 40 |
| 2 | 14 | 3 | 2 | 13 | 8 | 40 |
| 3 | 6 | 2 | 7 | 12 | 13 | 40 |
| 4 | 3 | 18 | 5 | 8 | 6 | 40 |
| Totals | 25 | 25 | 28 | 47 | 35 | 160 |
| Stack length | makenull | top | pop | push | empty | Totals |
| undefined | 4 | 4 | ||||
| 0 | 11 | 27 | 15 | 53 | ||
| 1 | 5 | 6 | 14 | 15 | 9 | 49 |
| 2 | 5 | 7 | 9 | 3 | 5 | 29 |
| 3 | 6 | 3 | 2 | 2 | 13 | |
| 4 | 6 | 2 | 4 | 12 | ||
| 5-10 | 0 | |||||
| Totals | 25 | 25 | 28 | 47 | 35 | 160 |
| Seq | Values pushed | No. | |||||||||||||
| 1 | 658 | 544 | 923 | -508 | 709 | 560 | 816 | 810 | 149 | -179 | -328 | 1 | 490 | -451 | 14 |
2 |
-23 | -365 | 814 | -464 | -885 | -702 | 123 | -248 | -284 | 828 | 177 | 635 | -588 | 13 | |
3 |
557 | 113 | 942 | -918 | -233 | 616 | 223 | -95 | 238 | -634 | -262 | 590 | 12 | ||
4 |
217 | 539 | 496 | -377 | -848 | -239 | -233 | 331 | 8 | ||||||

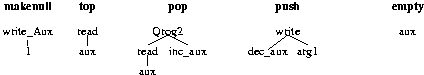
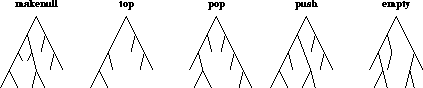
| Pseudo Code Definition of the Five Queue Operations | |||||
| [Aho et al.1987] | |||||
| Operation | Code | Comment | |||
| addone (i) | addone | := | (i + 1) % maxlength; | cyclic increment | |
| makenull | head | := | 0; | initialise queue | |
| tail | := | maxlength - 1; | |||
| empty | empty | := | (addone (tail) = head); | is queue empty? | |
| front | front | := | queue[ head ]; | front of queue | |
| enqueue( x) | tail | := | addone (tail); | add x to queue | |
| queue[ tail ] | := | x; | |||
| dequeue | dequeue | := | queue[ head ]; | return front | |
| head | := | addone (head); | and remove it | ||

Dequeue Read from head cell. Then increase head by one.
(provide default value, zero)
The six trees fall into categories:
Using categories primitives restricted to particular trees:
Memory usage penalty above 12 cells.
![[*]](cross_ref_motif.gif)
|
|
| Queue length | makenull | front | dequeue | enqueue | empty | Totals |
| undefined | 5 | 5 | ||||
| 0 | 10 | 27 | 16 | 53 | ||
| 1 | 4 | 9 | 14 | 18 | 7 | 52 |
| 2 | 4 | 12 | 11 | 8 | 7 | 42 |
| 3 | 9 | 6 | 7 | 5 | 27 | |
| 4 | 4 | 6 | 11 | 21 | ||
| 5 | 4 | 11 | 9 | 3 | 27 | |
| 6 | 8 | 9 | 11 | 5 | 33 | |
| 7 | 10 | 11 | 9 | 3 | 33 | |
| 8 | 3 | 9 | 4 | 16 | ||
| 9 | 5 | 4 | 2 | 11 | ||
| Totals | 23 | 64 | 81 | 104 | 48 | 320 |
| enqueue arguments | |||||||||||||||||||||||
| < | -10 | -9 | -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | > | |
| No. | 9 | 1 | 3 | 1 | 2 | 2 | 1 | 1 | 4 | 3 | 18 | 5 | 8 | 8 | 5 | 6 | 3 | 2 | 2 | 20 | |||
| Total | 104 | ||||||||||||||||||||||
| Objective | To evolve a first-in first-out queue | ||||||||||||
| Architecture | Five separate trees, plus single ADF | ||||||||||||
| Primitives |
|
||||||||||||
| Fitness Case | 4 test sequences, of 40 tests and
one of 160 (slide ![[*]](cross_ref_motif.gif) ) ) |
||||||||||||
| No program aborts | |||||||||||||
| Fitness Scaling | Each operation scored independently using Pareto comparison (1 per test passed), Memory usage above minimum (12 cells) penalized | ||||||||||||
| Selection | Pareto tournament of 4 | ||||||||||||
| Hits | Test passed | ||||||||||||
| Wrapper |
|
||||||||||||
| Parameters | Population = 10,000, G=100, program size |
||||||||||||
| Success Predicate | 320 hits, i.e. all tests passed |

Correct but requires infinite memory.
Very high ``effort''.
``easy'' 5 success in 11 (18) runs.
6 in 57 runs
3 non-general overfit test cases.

| Definitions of the Ten List Operations | |
| Makenull | Make the list an empty list and return position given by End. |
Retrieve( p) |
Return the element at position p. |
Insert( x, p) |
Insert x at position p, moving elements at p and following positions to the next higher position. |
Delete( p) |
Delete the element at position p, moving elements at p+1 and following positions to the previous lower position. |
End |
Return the position following the last element of the list. |
First |
Return the position of the first position. If the list is empty, return the position given by End. |
Next( p) |
Return the position following position p. |
Previous( p) |
Return the position before position p. |
Locate( x) |
Return the position of the first element containing value x. If x is not in the list at all then return the position given by End. |
Printlist |
Print the elements in their order of occurrence. |
Retrieve, Next, Previous, Adf1, Ins_adf, Del_adf, Loc_adf and
Prt_adf must contain arg1 terminal and Adf1 must
contain FUNC
(cf. slide ![[*]](cross_ref_motif.gif) )
)
(reduces runtime but encourage premature convergence?)
Assume later errors due to other code
![[*]](cross_ref_motif.gif)
(details given in [Langdon1995]).
| Objective | To evolve a list | ||||||||||||||||||||||||||||||
| Architecture | Ten separate trees, plus five ADFs | ||||||||||||||||||||||||||||||
| Primitives |
| ||||||||||||||||||||||||||||||
| All trees may contain +, -, 0, 1 and max |
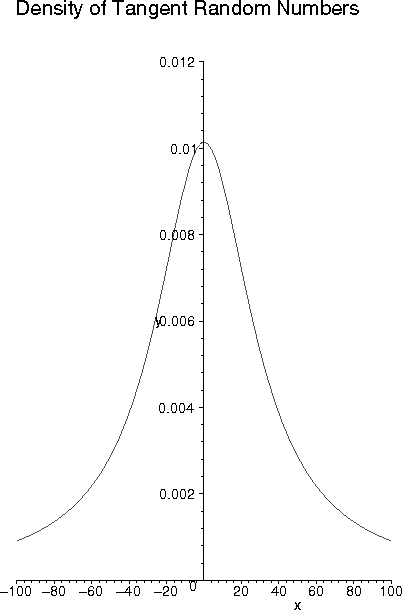
| Fitness Case | 538 trees run in 21 sequences. 167 consistency tests. Tangent test data distribution (F = 15). |
| Fitness Scaling | Each tree scored independently using Pareto comparison, memory usage above minimum (12 cells) and CPU usage above 120 per test run are Pareto fitness penalties. |
Selection |
Elitist Pareto Tournament group 4, Niche population sample size 81. |
| Hits | Number of consistency checks passed |
| Wrapper | Insert, Delete and Printlist result ignored, otherwise no wrapper. |
| Parameters | Population = 10,000, G=100, program size <501, Max initial tree size 50, 90% directed crossover. |
| Success Predicate | 167 hits, i.e. all tests passed |
| Primitive | Purpose |
| max | constant 10 ( |
| PROG2( t, u) | evaluate t; return u |
| arg1 | argument of current operation or ADF, but: |
| ARG1, ARG2 | arguments of Insert, Delete, Locate or Printlist. |
| aux1 | an auxiliary variable (i.e. in addition to indexed memory). |
| Set_Aux1( x) | aux1 = x; return aux1 |
| forwhile( s, e, l) | for i0 = s;
i0 |
| if timeout (32) exit loop | |
| if l returns zero exit loop | |
| return i0 | |
FUNC | call private ADF of operation which called Adf1. |
print( d) | if room in print buffer copy d into it; return number items in it |
| else evaluate d; return 0 | |
| read( x) | if | x |
| else return 0 | |
write( x, d) | if | x |
| else evaluate d; return 0 | |
swap( x, y) | if | x |
| if | x| > l and | y | |
| if | x | |
| return 1 |
| Treat as ADF | Returns value | Argu- ments | Pass-by-reference | Directly testable | Sufficient testing | |
| Makenull | ||||||
| Retrieve | 1 | |||||
| Insert | 2 | |||||
| Delete | 1 | |||||
| End | ||||||
| First | ||||||
| Next | 1 | |||||
| Previous | 1 | |||||
| Locate | 1 | |||||
| Printlist | ||||||
| Adf1 | 1 | |||||
| Ins_adf | 1 | |||||
| Del_adf | 1 | |||||
| Loc_adf | 1 | |||||
| Prt_adf | 1 | |||||

Chapter 8 discusses why primitives may become extinct.
![[*]](cross_ref_motif.gif) )
ensures crossovers are
allowed in every tree but are weighted towards the newly introduced
random code.
)
ensures crossovers are
allowed in every tree but are weighted towards the newly introduced
random code.
GP to evolve a recogniser for a Dyck language.
(, ), [, ], {, }, `, '.
Evolve to operate like pop, push and top?
All can be used by main tree
adf2 (top?) can be used by adf0.
ARG1 (integer representing current bracket), ifopen, ifmatch
aux1, Set_Aux1
![[*]](cross_ref_motif.gif) .
(stack given v. indexed memory plus inc_aux1, dec_aux1 and ADFs).
.
(stack given v. indexed memory plus inc_aux1, dec_aux1 and ADFs).
![[*]](cross_ref_motif.gif) .
.
| Objective | Find a program that classifies sequences of four types of bracket ( ( (represented as 5), ) (71), [ (13), ] (103), { (31), } (137), ` (43) and ' (167) ) as being correctly nested or not. | ||
| Primitives | Common | Stack Given | Index Memory |
| All trees: | ADD, SUB, PROG2, IFLTE, Ifeq, 0, 1, max, aux1 | Makenull, Empty, Top, Pop, Push | read, write, inc_aux1, dec_aux1 |
| rpb: as all plus | ifopen, ifmatch, ARG1, Set_Aux1 | adf1, adf2, adf3 | |
| adf1: as all plus | adf3 | ||
| adf2: as all plus | arg1, arg2 | ||
| Max prog size | Initial tree limit 50 | 50 | 4 x 50 = 200 |
| Fitness Case | 286 fixed test examples, cf. slide ![[*]](cross_ref_motif.gif) |
||
| Fitness Scaling | Number of correct answers returned. | ||
| Selection | Tournament size 4 (After first solution CPU penalty used giving a two dimensional fitness value, fitness niching used with a sample of up to 81 (9 x 9) nearest neighbours). | ||
| Hits | Number test symbols correctly classified. | ||
| Wrapper | Zero represents True (i.e. in language) and all other values False. | ||
| Parameters | Pop = 10,000, G = 50, Pareto, 3 x 3 demes, CPU penalty only after first solution found, Abort on first error in sentence. | ||
| Success predicate | Hits |
||
counting no. correctly classifies as correctly balanced or not.
![[*]](cross_ref_motif.gif) ).
).
| Len- | Positive | Negative | After Removing Duplicates | ||||||
| gth | Balanced | Rand | Positive | Balanced | Rand | Score | |||
| 1 | all 8 | 0 | |||||||
| 2 | all | 4 | all 60 | 9 | 18 | ||||
| 3 | 16 | 10 | 30 | ||||||
| 4 | all | 32 | all | 24 | 16 | 27 | 16 | 172 | |
| 5 | 16 | 16 | 80 | ||||||
| 6 | rand | 32 | rand | 32 | 32 | 32 | 32 | 32 | 576 |
| 7 | 16 | 16 | 112 | ||||||
| 8 | rand | 32 | rand | 32 | 32 | 32 | 32 | 32 | 768 |
| Totals | 91 | 112 | 83 | 1756 | |||||
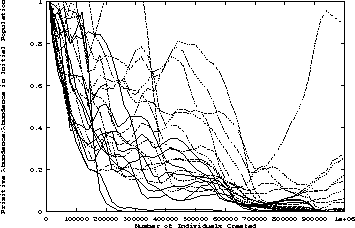
Some of the more promising runs were extended beyond 50 generations up to 140 generations without finding a solution.
| Objective | Find a program that evaluates integer Reverse Polish (postfix) arithmetic expressions. | ||
| Primitives | Common | Stack Given | Index Memory |
|
|
ADD, SUB, MUL, DIV, PROG2, 0, 1, aux1, Set_Aux1 | Top, Pop, Push | read, write, inc_aux1, dec_aux1, adf1, adf2 |
| num: as ops plus | arg1 | ||
| adf1: as ops but | no adfs | ||
| adf2: as ops but | no adfs and add arg1 | ||
| adf3: as ops but | no adfs and add arg1, arg2 | ||
| Max prog size | Initial tree limit 50 | 5 x 50 = 250 | 7 x 50 = 350 |
| Fitness Case | 127 fixed test expressions,
cf. slides ![[*]](cross_ref_motif.gif) , , ![[*]](cross_ref_motif.gif) and and ![[*]](cross_ref_motif.gif) . . | ||
| Fitness Scaling | Number of correct answers returned. | ||
| Selection | Pareto tournament size 4, CPU penalty (initial threshold 50 per operation), fitness niching used with a sample of up to 81 other members of the population. | ||
| Hits | Number of correct answers returned. | ||
| Wrapper | Value on num ignored. No wrapper on other trees. | ||
| Parameters | Pop = 10,000, G = 100, Pareto, no demes, CPU penalty (increased after 1st solution found), abort on first wrong answer given in expression. | ||
| Success predicate | Fitness | ||
Example: 1+2=3 correct
![]() Increment score of num and plus
Increment score of num and plus
| length | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | Total |
| No. of cases | 10 | 3 | 55 | 27 | 44 | 2 | 36 | 1 | 5 | 8 | 3 | 194 |
| Operation | No. | Max Score |
| num | 550 | 163 |
| plus | 67 | 58 |
| minus | 103 | 85 |
| times | 85 | 64 |
| divide | 156 | 127 |
| 420 | ||
| Totals | 970 | 497 |
| depth | 1 | 2 | 3 | 4 | 5 | 6 | Total |
| No. of cases | 387 | 390 | 149 | 31 | 12 | 1 | 970 |
| Actions Performed by Terminals and Functions | |
| Primitive | Purpose |
| DIV( x, y) | if y |
| else return 1 | |
| SUBR( x, y) DIVR( x, y) | As SUB and DIV except yield y- x and y/ x, i.e. operands reversed. |
| max | constant 10 ( |
| PROG2( t, u) | evaluate t; return u |
| ARG1, arg1, arg2 | arguments of current operation or ADF |
| aux1 | an auxiliary variable |
| Set_Aux1( x) | aux1 = x; return aux1 |
| ifopen( x, t1, t2) | if x = 5, 13, 31 or 43 return t1 //i.e. opening symbol |
| else return t2 | |
ifmatch( x, y, t1, t2) |
if x = 5, 13, 31 or 43 evaluate y //i.e. opening symbol |
| if ( x, y) = (5,71), (13,103), (31,137) or (43,167) return t1 | |
| else return t2 // x and y don't match | |
| else return t2 | |
| Makenull | clear stack; return 0 |
| Empty | if stack is empty return 0; else return 1 |
| Top | if stack is empty return 0; else return top of stack |
| Pop | if stack is empty return 0; else pop stack and return popped value |
| Push( x) | Evaluate x; |
| if < 99 items on stack push x; return x | |
| else return 0 | |
| read( x) | if | x |
| else return 0 | |
write( x, d) |
if | x |
| return original contents of store[ x] | |
| else evaluate d | |
| return 0 |
(PADO [Teller and Veloso1995,Teller1996] does not use problem specific data structures. Better than random performance on classification problems with no obvious structure).
Advice in [Kinnear, Jr.1994] and [Koza1992] remains sound, however:
However a high variety does not indicate all is well. Phenotypic (behaviour) variation may also be useful.
The population can be compressed, e.g. using gzip. Compression to <1 bit per primitive
The key to successful human produced software is using abstraction to control the complexity of each task in hand.
While GP work to date has concentrated on functional abstraction (ADFs etc.), GP must also to take advantage of data abstraction