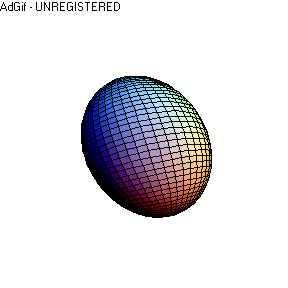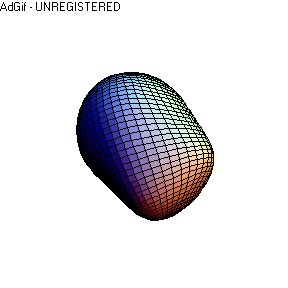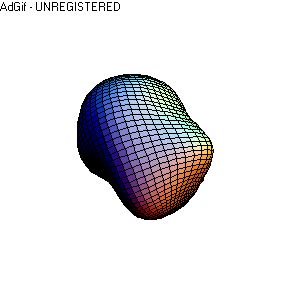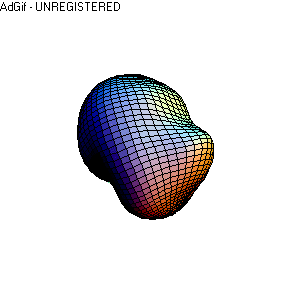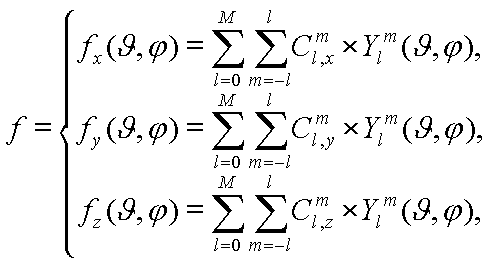The
routine use of 3D imaging methods by the medical community, such as MRI
and CT is creating a vast amount of volumetric data. The usual way of storing
these data is voxel images that allow visual capturing of the objects, but
lack structural description since they are based on huge lists of numbers.On
the other hand new medical imaging modalities, such as Optical Tomography
require precise and smooth models of human tissues (e.g. baby’s head) for
the solution of the inverse and forward problem. Until now the models used
in such applications are rough polygon meshes based on voxel images. We
demonstrate a method to create a parametric model of a body structure by
mapping the surface to a sphere. Basis functions like spherical harmonics
can be used for a description of the surface.
Parametric Description
of 3-Dimensional Surfaces
using
Spherical Harmonics
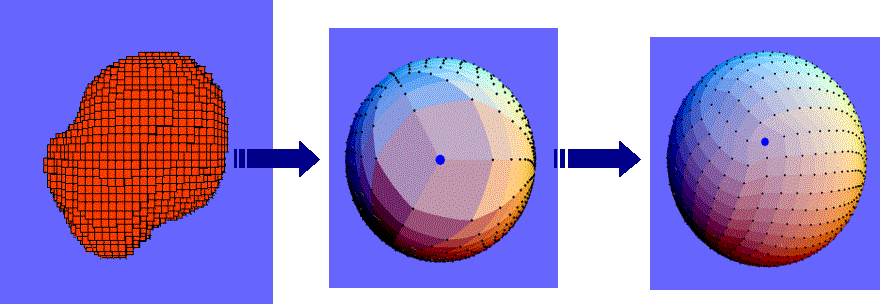
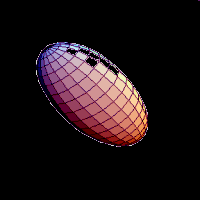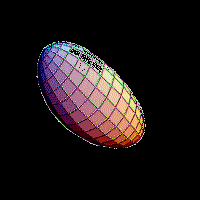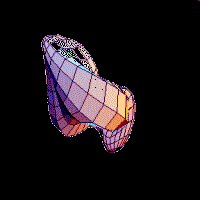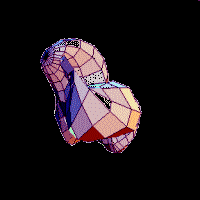
The
closed surface extracted from a baby’s head voxel image is topologically equivalent
to a sphere, therefore it can be mapped on a sphere’s surface. The construction
of this homeomorphism from the closed surface to the unit sphere results in
a parametric representation of the surface. Diffusion of the surface nodes is
used for an initial mapping and then constrained non-linear optimisation method
to achieve the necessary one-to-one mapping between the two surfaces. The square
faces from the voxel object have been mapped on the sphere’s surface. Two parameters
Theta and Fi have been assigned for each node of the head’s surface. For every
point on the head’s surface a unique pair of parameters has been assigned.
Using
weighted basis functions also described on the sphere, such as the Spherical
Harmonics we can reconstruct the shape of the voxel object to any desired level
of detail
Having
defined the Spherical Harmonics weighting coefficients [Cx, Cy , Cz], the surface
is now described, by the parametric function f (theta,fi):