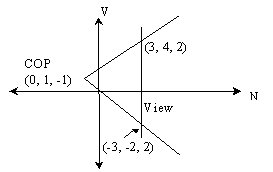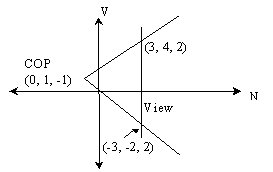Exercises Chapter 9

1. Give the transformation matrices that can turn the following arrangement to a canonical perspective.

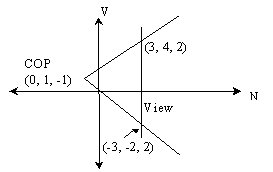2. Suppose that a canonical perspective space is defined as follows: It is a left handed system as usual, the COP is at (0,0,-1), the viewplane distance is zero (ie, the viewplane is the xy plane through the origin), and the view plane window is the triangle defined by (1,1,0), (-1,1,0) and (0,-1,0). No front and back clipping planes are specified.

2(a). What are the plane equations of the three bounding planes of this view volume?

2(b). The usual clipping region for x and y in perspective space can be expressed as -z <= x <= z, and -z <= y <= z. Express this new clipping region in a similar form, using inequalities.

2(c). Clip the polygon (1,3,2), (-1,0,2), (0,0,0) against the defined viewing volume.

Back to: Index of Exercises
Back to: Chapter 9

Last modified: Tue Oct 02 09:33:55 GMT Daylight Time 2001